题目内容
如图，⊙O的直径AB=4，半径OC⊥AB，D为弧BC上一点，DE⊥OC，DF⊥AB，垂足分别为E、F．则EF=考点：矩形的判定与性质,圆的认识
专题：
分析：求出圆的半径，再判断出四边形OFDE是矩形，然后根据矩形的对角线相等解答即可．
解答：解：∵⊙O的直径AB=4，
∴圆的半径为4÷2=2，
∵OC⊥AB，DE⊥OC，DF⊥AB，
∴四边形OFDE是矩形，
∴EF=OD=2．
故答案为：2．
∴圆的半径为4÷2=2，
∵OC⊥AB，DE⊥OC，DF⊥AB，
∴四边形OFDE是矩形，
∴EF=OD=2．
故答案为：2．
点评：本题考查了矩形的判定与性质，圆的认识，考虑利用矩形的对角线相等把EF转化为OD是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
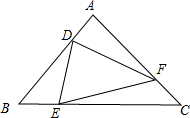等边△ABC边长为1，D、E、F分别在边AB、BC、CA上，△DEF也是等边三角形．
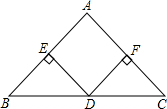如图，在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别为E、F．只添加一个条件，使四边形EDFA是正方形．请你至少写出两种不同的添加方法．并选择一种证明．抛物线y=x2-4与x轴交于B，C两点，顶点为A，则△ABC的周长为（ ）
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
如图，在△ABC中，∠B比∠BAC大35°，∠C=65°，AD平分∠BAC交AB于D，DE⊥AB于E，求∠ADE的度数．下列函数中，反比例函数是（ ）
| A、y=x-1 | ||
B、y=
| ||
C、y=
| ||
D、y=
|