题目内容
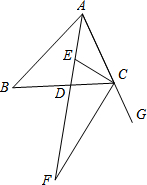 如图,△ABC中,AD为角平分线,E为AD上一点,且EC平分∠ACB,CF是△ABC的外角∠BCG的平分线,交AD延长线于F,∠F=20°,∠ACB-∠B=30°,求△ABC的三个内角的大小.
如图,△ABC中,AD为角平分线,E为AD上一点,且EC平分∠ACB,CF是△ABC的外角∠BCG的平分线,交AD延长线于F,∠F=20°,∠ACB-∠B=30°,求△ABC的三个内角的大小.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的定义可得∠FAC=
∠BAC,∠FCG=
∠BCG,再根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BCG=∠B+∠BAC,∠FCG=∠F+∠FAC,然后整理得到∠F=
∠B,然后代入数据求出∠B,再求出∠ACB,然后根据三角形的内角和定理列式求出∠BAC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵AD为角平分线,CF是△ABC的外角∠BCG的平分线,
∴∠FAC=
∠BAC,∠FCG=
∠BCG,
由三角形的外角性质得,∠BCG=∠B+∠BAC,∠FCG=∠F+∠FAC,
∴
(∠B+∠BAC)=∠F+∠FAC=∠F+
∠BAC,
∴∠F=
∠B,
∵∠F=20°,
∴∠B=2∠F=2×20°=40°,
∵∠ACB-∠B=30°,
∴∠ACB=30°+40°=70°,
在△ABC中,∠BAC=180°-40°-70°=70°.
∴∠FAC=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠BCG=∠B+∠BAC,∠FCG=∠F+∠FAC,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴∠F=
| 1 |
| 2 |
∵∠F=20°,
∴∠B=2∠F=2×20°=40°,
∵∠ACB-∠B=30°,
∴∠ACB=30°+40°=70°,
在△ABC中,∠BAC=180°-40°-70°=70°.
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,求出∠F=
∠B是解题的关键.
| 1 |
| 2 |

练习册系列答案
相关题目
下列函数中,反比例函数是( )
| A、y=x-1 | ||
B、y=
| ||
C、y=
| ||
D、y=
|
 等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形.
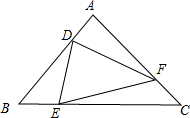
等边△ABC边长为1,D、E、F分别在边AB、BC、CA上,△DEF也是等边三角形. 如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.
如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.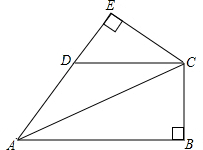 已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.
已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.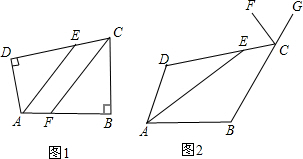 在四边形ABCD中,∠B=∠D=α.
在四边形ABCD中,∠B=∠D=α.