题目内容
把代数式(a2-2ab+b2+5)(-a2+2ab-b2+5)写成(5+m)(5-m)的形式,并求出m.
考点:去括号与添括号
专题:
分析:根据式子的特点变形得出[5+(a2-2ab+b2)][5-(a2-2ab+b2)],即可得出答案.
解答:解:(a2-2ab+b2+5)(-a2+2ab-b2+5)
=[5+(a2-2ab+b2)][5-(a2-2ab+b2)]
即m=a2-2ab+b2
=[5+(a2-2ab+b2)][5-(a2-2ab+b2)]
即m=a2-2ab+b2
点评:本题考查了去括号和添括号法则的应用,题目比较好,难度不大.

练习册系列答案
相关题目
抛物线y=x2-4与x轴交于B,C两点,顶点为A,则△ABC的周长为( )
A、4
| ||
B、4
| ||
| C、12 | ||
D、2
|
下列说法错误的是( )
| A、矩形的对角线互相平分 |
| B、矩形的对角线相等 |
| C、有一个角是直角的四边形是矩形 |
| D、有一个角是直角的平行四边形叫做矩形 |
 已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现?
已知∠B=∠C=90°,M是BC的中点,MN⊥AD,若∠1=∠2,求证:∠3=∠4,你还有什么发现? 如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.
如图,在△ABC中,∠B比∠BAC大35°,∠C=65°,AD平分∠BAC交AB于D,DE⊥AB于E,求∠ADE的度数.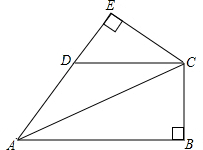 已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.
已知∠B=∠E=90°,CE=CB,AB∥CD,求证:AD=CD.