Question

1．如图1，△ABC中，AD是∠BAC的平分线，若AB=AC+CD，那么∠ACB与∠ABC有怎样的数量关系？小明通过观察分析，形成了如下解题思路：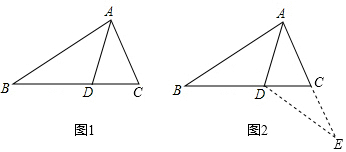

如图2，延长AC到E，使CE=CD，连接DE．由AB=AC+CD，可得AE=AB．又因为AD是∠BAC的平分线，可得△ABD≌△AED，进一步分析就可以得到∠ACB与∠ABC的数量关系．
（1）判定△ABD与△AED全等的依据是SAS；
（2）∠ACB与∠ABC的数量关系为：∠ACB=2∠ABC．

Answer 1

分析 （1）根据已知条件即可得到结论；
（2）根据全等三角形的性质和等腰三角形的性质即可得到结论．

解答 解：（1）SAS；
（2）∵△ABD≌△AED，
∴∠B=∠E，
∵CD=CE，
∴∠CDE=∠E，
∴∠ACB=2∠E，
∴∠ACB=2∠ABC．
故答案为：SAS，∠ACB=2∠ABC．

点评 本题考查了等腰三角形的性质，全等三角形的判定和性质，熟练掌握等腰三角形的性质是解题的关键．