题目内容
12.观察下列按规律排列的数据,1,$-\frac{3}{4}$,$\frac{1}{2}$,$-\frac{7}{16}$,…,则第n(n为正整数)个式子是(-1)n-1•$\frac{2n-1}{{n}^{2}}$.分析 分子是从1开始连续的奇数,分母是从1开始连续自然数的平方,奇数位置为正,偶数位置为负,由此得出第n个数为(-1)n-1•$\frac{2n-1}{{n}^{2}}$,由此进一步计算得出答案即可.
解答 解:数列为1,$-\frac{3}{4}$,$\frac{1}{2}$,$-\frac{7}{16}$,…,第n个数为(-1)n-1•$\frac{2n-1}{{n}^{2}}$.
故答案为(-1)n-1•$\frac{2n-1}{{n}^{2}}$.
点评 本题是对数字变化规律的考查,确定从分子、分母和正负情况三个方面考虑求解是解题的关键.

练习册系列答案
相关题目
2.下列命题中,假命题的是( )
| A. | 分别有一个角是110°的两个等腰三角形相似 | |
| B. | 如果两个三角形相似,则他们的面积比等于相似比 | |
| C. | 若5x=8y,则$\frac{x}{y}$=$\frac{8}{5}$ | |
| D. | 有一个角相等的两个菱形相似 |
2.如果x=2是方程$\frac{1}{2}$x-a=-1的解,那么a的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -6 |
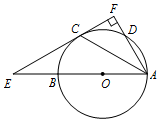 如图,AB是⊙O的直径,C,D是⊙O上两点,且$\widehat{BC}$=$\widehat{CD}$,过点C的直线CF⊥AD于点F,交AB的延长线于点E,连接AC.
如图,AB是⊙O的直径,C,D是⊙O上两点,且$\widehat{BC}$=$\widehat{CD}$,过点C的直线CF⊥AD于点F,交AB的延长线于点E,连接AC.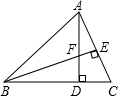 如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.