题目内容
13.已知一扇形的面积是24π,圆心角是60°,则这个扇形的半径是12.分析 把已知数据代入扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$,计算即可.
解答 解:设这个扇形的半径是为R,
则$\frac{60π×{R}^{2}}{360}$=24π,
解得,R=12,
故答案为:12.
点评 本题考查的是扇形面积的计算,掌握扇形的面积公式S=$\frac{nπ{R}^{2}}{360}$是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.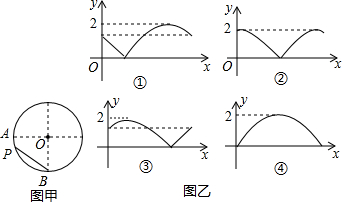 如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )
如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )
 如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )
如图甲,A、B是半径为1的⊙O上两点,且OA⊥OB.点P从A出发,在⊙O上以每秒一个单位的速度匀速运动,回到点A运动结束.设运动时间为x,弦BP的长度为y,那么如图乙图象中可能表示y与x的函数关系的是( )| A. | ① | B. | ④ | C. | ①或③ | D. | ②或④ |
2.如果x=2是方程$\frac{1}{2}$x-a=-1的解,那么a的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | -6 |
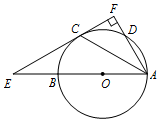 如图,AB是⊙O的直径,C,D是⊙O上两点,且$\widehat{BC}$=$\widehat{CD}$,过点C的直线CF⊥AD于点F,交AB的延长线于点E,连接AC.
如图,AB是⊙O的直径,C,D是⊙O上两点,且$\widehat{BC}$=$\widehat{CD}$,过点C的直线CF⊥AD于点F,交AB的延长线于点E,连接AC.