题目内容
2.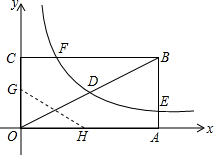 如图,矩形OABC的边长OA=8,顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E、F,且tan∠BOA=$\frac{1}{2}$.
如图,矩形OABC的边长OA=8,顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$(k≠0)在第一象限内的图象经过点D、E、F,且tan∠BOA=$\frac{1}{2}$.(1)求边AB的长;
(2)求反比例函数的解析式及F点坐标;
(3)若反比例函数的图象与矩形的边BC交于点F,将矩形折叠,使点O与点F重合,折叠分别与x、y轴正半轴交于点H、G,求线段OG的长.
分析 (1)在Rt△AOB中,由三角函数的定义可求得AB的长;
(2)由矩形的性质可求得B点坐标,则可求得D点坐标,代入反比例函数解析式可求得k的值,则可求得F点的坐标;
(3)连接FG,设OG=t,则FG=t,CG=4-t,在Rt△CGF中由勾股定理可得到关于t的方程,可求得t的值,即可求得OG的长.
解答 解:
(1)在Rt△AOB中,
∵tan∠BOA=$\frac{1}{2}$,
∴AB=OA•tan∠BOA=8×$\frac{1}{2}$=4;
(2)由(1)可知B点坐标为(8,4),
∵D为OB的中点,
∴D(4,2),
∵反比例函数y=$\frac{k}{x}$图象过点D,
∴k=4×2=8,
∴反比例函数解析式为y=$\frac{8}{x}$,
设F(a,4),
∵反比例函数图象与矩形的边BC交于点F,
∴4a=8,解得a=2,
∴F(2,4);
(3)连接FG,如图,
∵F(2,4),
∴CF=2,
设OG=t,则OG=FG=t,CG=4-t,
在Rt△CGF中,由勾股定理可得GF2=CF2+CG2,即t2=(4-t)2+22,解得t=$\frac{5}{2}$,
∴OG=$\frac{5}{2}$.
点评 本题为反比例函数的综合应用,涉及矩形的性质、待定系数法、三角函数的定义、勾股定理、折叠的性质及方程思想等知识.在(1)中掌握三角函数的定义是解题的关键,在(2)中求得D点的坐标是解题的关键,在(3)中利用折叠的性质在直角三角形中应用勾股定理得到关于OG的方程是解题的关键.本题考查知识点较多,综合性较强,难度适中.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
12.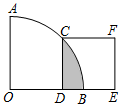 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
 如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )
如图,在扇形OAB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,若正方形CDEF的边长为2,则图中阴影部分的面积为( )| A. | π-2 | B. | 2π-2 | C. | 4π-4 | D. | 4π-8 |
17.下列图形中,∠1与∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
14.计算(x3)2的结果是( )
| A. | x8 | B. | x5 | C. | 3x2 | D. | x6 |
11.已知∠1与∠2是同位角,则( )
| A. | ∠1=∠2 | B. | ∠1>∠2 | C. | ∠1<∠2 | D. | 以上都有可能 |
12.当5个整数从小到大排列,其中位数是4,如果这组数据的唯一众数是6,则5个整数的和最大是( )
| A. | 21 | B. | 22 | C. | 23 | D. | 24 |