题目内容
16．
如图，抛物线为二次函数y=x2-4x的图象．（1）抛物线顶点A的坐标是（2，-4）；
（2）抛物线与x轴的交点的坐标是（0，0）和（4，0）；
（3）通过观察图象，写出x2-4x＞0时x的取值范围．
分析 （1）通过配方法即可求出顶点坐标．
（2）令y=0，求出x的值即可求出抛物线与X轴的交点坐标．
（3）满足x2-4x＞0图象在x轴上方，根据图象可以得到解决．
解答 解：（1）∵y=x2-4x=（x2-4x+4）-4=（x-2）2-4
∴顶点为（2，-4），
故答案为（2，-4）．
（2）令y=0得到x2-4x=0，
∴x（x-4）=0
∴x=0或4
∴抛物线与X轴交点为（0，0）和（4，0），
故答案为（0，0）和（4，0）．
（3）由图象可知：x＞4或x＜0．
点评 本题考查二次函数的有关知识，必须熟练掌握配方法求顶点坐标以及求抛物线与x轴交点的坐标的方法，学会利用数形结合的思想确定自变量的取值范围．
练习册系列答案
相关题目
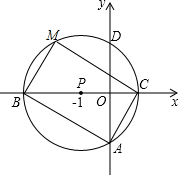如图，以点P（-1，0）为圆心的圆，交x轴于B、C两点（B在C的左侧），交y轴于A、D两点（A在D的下方），AD=2$\sqrt{3}$，将△ABC绕点P旋转180°，得到△MCB．
如图1，是抛物线y=ax2+bx+c（a≠0）图象的一部分，已知抛物线的对称轴为直线x=2，与x轴的一个交点是（-1，0）；