题目内容
6.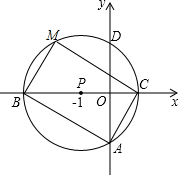 如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2$\sqrt{3}$,将△ABC绕点P旋转180°,得到△MCB.
如图,以点P(-1,0)为圆心的圆,交x轴于B、C两点(B在C的左侧),交y轴于A、D两点(A在D的下方),AD=2$\sqrt{3}$,将△ABC绕点P旋转180°,得到△MCB.(1)求B、C两点的坐标;
(2)点E是线段MC(不包括两端点)上的动点,连接BE,点Q为BE的中点,过点E作EG⊥BC于G,连接MQ、QG.在点E运动过程中,∠MQG的大小是否发生变化?如果发生变化,说明理由;如果不变,求出∠MQG的度数.
分析 (1)通过垂径定理,求出圆的半径,结合点P的坐标即可求出点B、点C的坐标;
(2)由旋转性质和点的坐标,可以求出三角形ABC和三角形BCM所有角的度数,利用点的坐标和相应角的度数判定点E、M、B、G在以点Q为圆心,QB为半径的圆上,进而可以求出∠MQG=2∠MBG=120°.
解答 解:(1)连接PA:
∵PO⊥AD,
∴AO=DO.
∵AD=2$\sqrt{3}$,
∴OA=$\sqrt{3}$.
∵点P坐标为(-1,0),
∴OP=1.
∴PA=2.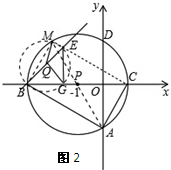
∴BP=CP=2.
∴B(-3,0),C(1,0).
(2)∠MQG的大小不发生变化,∠MQG=120°.
∵△ABC绕点P旋转180°,
∴∠BMC=90°.∠MBC=∠BCA
∵∠COA=90°,OC=1,OA=$\sqrt{3}$,
∴tan∠OCA=$\sqrt{3}$.
∴∠OCA=60°.
∴∠MBC=∠BCA=60°.
∵EG⊥BO,
∵∠BGE=90°.
∴∠BMC=∠BGE=90°.
∵点Q是BE的中点,
∴QM=QE=QB=QG.
∴点E、M、B、G在以点Q为圆心,QB为半径的圆上,如图2所示.
∴∠MQG=2∠MBG=120°.
点评 题目考查了圆的综合性质,通过圆与三角形旋转的结合,考查学生对圆综合性质的考查,题目整体较难,适合学生课后培优训练.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.在方程3x-y=2;2y-$\frac{1}{3}$=-1;2a=1;$\frac{4}{x}$-2=0;$\frac{x+1}{2}$-$\frac{1}{3}$x=2中,一元一次方程的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,三角形ABC的面积为8cm2,点D、E分别在边BC、AC上,BE交AD于点F,若BD=CD,AF=3FD,则三角形ABD的面积是4cm2,三角形DEF的面积是0.6cm2.
如图,三角形ABC的面积为8cm2,点D、E分别在边BC、AC上,BE交AD于点F,若BD=CD,AF=3FD,则三角形ABD的面积是4cm2,三角形DEF的面积是0.6cm2. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论:
已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1.有位学生写出了以下五个结论: 如图,抛物线为二次函数y=x2-4x的图象.
如图,抛物线为二次函数y=x2-4x的图象.