题目内容
14.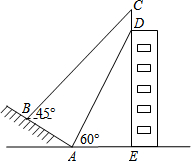 如图,一个坡度i=1:$\sqrt{3}$的小山坡,坡前高楼DE的顶端竖立一块广告牌CD,张强在山坡上点B处测量广告牌的顶端C的仰角为45°,在坡底点A处测量广告牌的底端D的仰角为60°,AB=12米,AE=18米,求这块广告牌CD的高度.(点A,B,C,D,E在同一平面内,测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,一个坡度i=1:$\sqrt{3}$的小山坡,坡前高楼DE的顶端竖立一块广告牌CD,张强在山坡上点B处测量广告牌的顶端C的仰角为45°,在坡底点A处测量广告牌的底端D的仰角为60°,AB=12米,AE=18米,求这块广告牌CD的高度.(点A,B,C,D,E在同一平面内,测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
分析 首先作BF⊥DE于点F,BG⊥AE于点G,得出四边形BGEF为矩形,进而求出CF,EF,DE的长,进而得出答案.
解答 解:作BF⊥DE于点F,BG⊥AE于点G,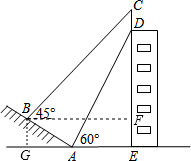
∵CE⊥AE,
∴四边形BGEF为矩形,
∴BG=EF,BF=GE,
在Rt△ADE中,
∵tan∠ADE=$\frac{DE}{AE}$,
∴DE=AE•tan∠ADE=18$\sqrt{3}$,
∵山坡AB的坡度i=1:$\sqrt{3}$,AB=12,
∴BG=6,AG=6$\sqrt{3}$,
∴EF=BG=6,BF=AG+AE=6$\sqrt{3}$+18,
∵∠CBF=45°
∴CF=BF=6$\sqrt{3}$+18,
∴CD=CF+EF-DE=6$\sqrt{3}$+18+6-18$\sqrt{3}$≈24-12×1.732≈3.2(m),
答:这块宣传牌CD的高度为3.2米.
点评 此题主要考查了解直角三角形的应用,根据已知熟练掌握锐角三角函数关系得出CF的长是解题关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
4. 随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
请根据统计图中提供的信息,解答下列问题:
(1)本次接受调查的总人数是200人;
(2)通过计算,将条形统计图补充完整;
(3)扇形统计图中,观点“D”的百分比是24%,“B”所对应的圆心角的度数是126°;
(4)估算在全校3000名学生中,对“低头族”表示不赞同的人数.
 随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).
随着智能手机的普及,QQ、微博、微信等新型社交平台的兴起,在公共场所的“低头族”越来越多,针对“您如何人看待低头族”的问题,晨光数学小组在全校范围内进行了随机调查,发放了调查问卷,并将调查结果绘制成了如图所示的统计图表(均不完整).| 您如何看待“低头族”的调查问卷 您好!这是一份关于您如何看待低头族的问卷调查表,请在表格内选择一项您最认同的观点,在其后的空格内打对勾,感谢您的参与! | ||
| 代码 | 观点 | 您的选择 |
| A | 获取信息方便 | |
| B | 联系朋友方便 | |
| C | 对视力不好,影响健康 | |
| D | 使朋友亲人疏远,不利于交流 | |
(1)本次接受调查的总人数是200人;
(2)通过计算,将条形统计图补充完整;
(3)扇形统计图中,观点“D”的百分比是24%,“B”所对应的圆心角的度数是126°;
(4)估算在全校3000名学生中,对“低头族”表示不赞同的人数.
9.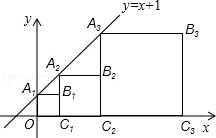 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B2016的纵坐标是( )| A. | 22013 | B. | 22014 | C. | 22015 | D. | 22016 |
19.下列各式由左边到右边的变形,属于因式分解的是( )
| A. | (x+1)(x-1)=x2-1 | B. | x2+2x+1=x(x+2)+1 | C. | a2-4b2=(a+2b)(a-2b) | D. | a(x-y)=ax-ay |
6.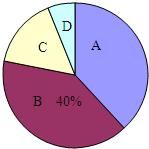 某市共有45000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
某市共有45000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
请你根据以上图表提供的信息,解答下列问题:
(1)m=20,n=8,x=0.4,y=0.16;
(2)在扇形图中,C等级所对应的圆心角是57.6度;
(3)如果该校九年级共有500名男生,则其中成绩等级达到优秀和良好的共有多少人?
 某市共有45000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:
某市共有45000余名学生参加中考体育测试,为了了解九年级男生立定跳远的成绩成绩,从某校随机抽取了50名男生的测试成绩,根据测试评分标准,将他们的得分按优秀、良好、及格、不及格(分别用A、B、C、D表示)四个等级进行统计,并绘制成扇形图和统计表:| 等级 | 成绩(分) | 频数(人数) | 频率 |
| A | 90~100 | 19 | 0.38 |
| B | 75~89 | m | x |
| C | 60~74 | n | y |
| D | 60以下 | 3 | 0.06 |
| 合计 | 50 | 1.00 |
(1)m=20,n=8,x=0.4,y=0.16;
(2)在扇形图中,C等级所对应的圆心角是57.6度;
(3)如果该校九年级共有500名男生,则其中成绩等级达到优秀和良好的共有多少人?
3. 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )| A. | (504,504) | B. | (-504,504) | C. | (-504,-504) | D. | (504,-504) |
4.以下列长度(单位:cm)为边长的三角形是直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,9 | C. | 6,12,13 | D. | 8,15,17 |
