题目内容
3. 如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )
如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8,…,顶点一次用A1,A2,A3,A4,…表示,则顶点A2016的坐标是( )| A. | (504,504) | B. | (-504,504) | C. | (-504,-504) | D. | (504,-504) |
分析 根据正方形的性质写出部分An的坐标,根据坐标的变化找出变化规律“A4n+1(-n-1,-n-1),A4n+2(-n-1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,-n-1)(n为自然数)”,依此规律即可得出结论.
解答 解:观察,发现规律:
A1(-1,-1),A2(-1,1),A3(1,1),A4(1,-1),A5(-2,-2),A6(-2,2),A7(2,2),A8(2,-2),A9(-3,-3),…,
∴A4n+1(-n-1,-n-1),A4n+2(-n-1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,-n-1)(n为自然数).
∵2016=503×4+4,
∴A2016的坐标是(503+1,-503-1),即(504,-504).
故选D.
点评 本题考查了规律型中点的坐标,解题的关键是找出点坐标的变化规律“A4n+1(-n-1,-n-1),A4n+2(-n-1,n+1),A4n+3(n+1,n+1),A4n+4(n+1,-n-1)(n为自然数)”.本题属于基础题,难度不大,解决该题型题目时,列出部分点的坐标,根据坐标的变化找出变化规律是关键.

练习册系列答案
相关题目
18.一元二次方程x2-2x+m=0总有实数根,则m应满足的条件是( )
| A. | m=1 | B. | m≥1 | C. | m<1 | D. | m≤1 |
8.下列各式计算正确的是( )
| A. | 2$\sqrt{3}$×3$\sqrt{3}$=6$\sqrt{3}$ | B. | $\sqrt{28}$$÷\sqrt{7}$=2 | C. | $\sqrt{3}$+$\sqrt{7}$=$\sqrt{10}$ | D. | 5$\sqrt{3}$-3$\sqrt{3}$=2 |
15.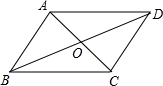 如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
 如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )
如图,在平行四边形ABCD中,AC与BD相交于点O,AB⊥AC,∠DAC=45°,AC=2,则BD的长为( )| A. | 6 | B. | 2$\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 3 |

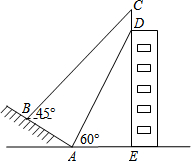 如图,一个坡度i=1:$\sqrt{3}$的小山坡,坡前高楼DE的顶端竖立一块广告牌CD,张强在山坡上点B处测量广告牌的顶端C的仰角为45°,在坡底点A处测量广告牌的底端D的仰角为60°,AB=12米,AE=18米,求这块广告牌CD的高度.(点A,B,C,D,E在同一平面内,测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,一个坡度i=1:$\sqrt{3}$的小山坡,坡前高楼DE的顶端竖立一块广告牌CD,张强在山坡上点B处测量广告牌的顶端C的仰角为45°,在坡底点A处测量广告牌的底端D的仰角为60°,AB=12米,AE=18米,求这块广告牌CD的高度.(点A,B,C,D,E在同一平面内,测角器的高度忽略不计,结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)



