题目内容
11.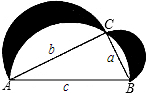 如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
分析 阴影部分面积可以看成是以AC、BC为直径的两个半圆的面积加上一个直角三角形ABC的面积减去一个以AB为直径的半圆的面积.
解答 解:S阴影=直径为AC的半圆的面积+直径为BC的半圆的面积+S△ABC-直径为AB的半圆的面积,
=$\frac{1}{2}$π$(\frac{AC}{2})^{2}$+$\frac{1}{2}$π$(\frac{BC}{2})^{2}$+$\frac{1}{2}$AC×BC-$\frac{1}{2}$π$(\frac{AB}{2})^{2}$,
=$\frac{1}{8}$π(AC)2+$\frac{1}{8}$π(BC)2-$\frac{1}{8}$π(AB)2+$\frac{1}{2}$AC×BC,
=$\frac{1}{8}$π(AC2+BC2-AB2)+$\frac{1}{2}$AC×BC,
=$\frac{1}{2}$AC×BC,
所以阴影部分的面积与直角三角形的面积相等.
点评 此题主要考查了扇形面积的计算公式,阴影部分的面积可以看作是几个规则图形的面积的和或差.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
1.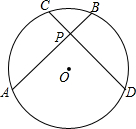 如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
 如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )
如图1,在⊙O中,弦AB与CD交于点P,若AB=CD,则$\widehat{AC}$与$\widehat{BD}$的大小关系是( )| A. | $\widehat{AC}$=$\widehat{BD}$ | B. | $\widehat{AC}$$>\widehat{BD}$ | C. | $\widehat{AC}$$<\widehat{BD}$ | D. | 不能确定 |
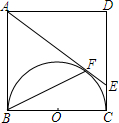 如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:
如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:
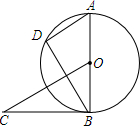 如图,⊙O的直径AB=6,BC切⊙O于B,OC∥AD,BC=4,求弦AD的长.
如图,⊙O的直径AB=6,BC切⊙O于B,OC∥AD,BC=4,求弦AD的长.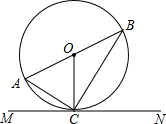 直线MN切⊙O于点C,AB是⊙O的直径且∠CAB=53°,则∠BOC=106°,∠ACB=90°,∠ACM=37°,∠BCN=53°.
直线MN切⊙O于点C,AB是⊙O的直径且∠CAB=53°,则∠BOC=106°,∠ACB=90°,∠ACM=37°,∠BCN=53°.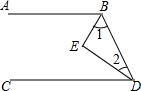 如图,BE、DE分别平分∠ABD和∠CDB,∠1+∠2=90°,问AB与CD平行吗?说明理由.
如图,BE、DE分别平分∠ABD和∠CDB,∠1+∠2=90°,问AB与CD平行吗?说明理由.