题目内容
19.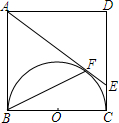 如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:
如图,正方形ABCD的边长为4cm,以正方形的边BC为直径在正方形内作半圆,再经过A点作半圆的切线AE,与半圆相切于F点,与DC相交于E点,求:(1)△ADE的面积;
(2)求线段BF的长.
分析 (1)由于AE与圆O切于点F,根据切线长定理有AF=AB=4cm,EF=EC;设EF=EC=xcm.则DE=(4-x)cm,AE=(4+x)cm,然后在三角形BCE中由勾股定理可以列出关于x的方程,解方程即可求出,然后就可以求出△ADE的面积;
(2)连接OF,OA,OA与BF交于G,如图,根据正方形的性质得∠ABC=90°,利用切线的判定方法可得到AB为⊙O的切线,再根据切线长定理得到AB=AF,OA平分∠BAF,则根据等腰三角形的性质得到AG⊥BF,BG=FG,然后根据勾股定理得OA=2$\sqrt{5}$,再利用面积法计算出BG=$\frac{4\sqrt{5}}{5}$,则BF=2BG=$\frac{8\sqrt{5}}{5}$.
解答 解:(1)∵AE与圆O切于点F,
∴AF=AB=4cm,EF=EC,
设EF=EC=xcm,
则DE=(4-x)cm,AE=(4+x)cm,
在三角形ADE中由勾股定理得:
(4-x)2+42=(4+x)2,
∴x=1cm,
∴CE=1cm,
∴DE=4-1=3cm,
∴S△ADE=AD•DE÷2=3×4÷2=6cm2;
(2)连接OF,OA,OA与BF交于G, 如图,
如图,
∵四边形ABCD为正方形,
∴∠ABC=90°,
而BC为⊙O的直径,
∴AB为⊙O的切线,
∵AF与半圆相切于点,
∴AB=AF,OA平分∠BAF,
∴AG⊥BF,
∴BG=FG,
在Rt△ABO中,∵OB=2,AB=4,
∴OA=$\sqrt{O{B}^{2}+A{B}^{2}}$=2$\sqrt{5}$,
∵$\frac{1}{2}$BG•OA=$\frac{1}{2}$OB•AB,
∴BG=$\frac{2×4}{2\sqrt{5}}$=$\frac{4\sqrt{5}}{5}$,
∴BF=2BG=$\frac{8\sqrt{5}}{5}$.
点评 考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了切线长定理.注意构造直角三角形,利用勾股定理计算线段的长.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案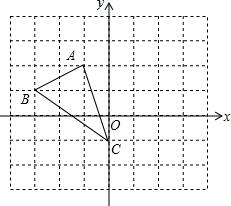 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(0,-1).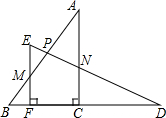 将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.
将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.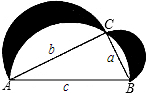 如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.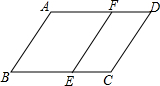 如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?
如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?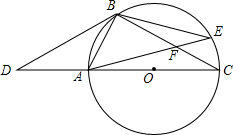 如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.
如图,点D是⊙O的直径CA延长线上的一点,点B在⊙O上,且AB=AD=AO.