题目内容
16.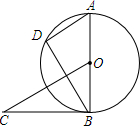 如图,⊙O的直径AB=6,BC切⊙O于B,OC∥AD,BC=4,求弦AD的长.
如图,⊙O的直径AB=6,BC切⊙O于B,OC∥AD,BC=4,求弦AD的长.
分析 只要证明△CBO∽△BDA得$\frac{BO}{AD}$=$\frac{CO}{AB}$,利用勾股定理求出CO,即可解决问题.
解答 解:∵AB是⊙O直径,
∴∠D=90°,
∵BC切⊙O于B,
∴AB⊥BC,∠CBO=90°,
在RT△BCO中,∵∠CBO=90°,BC=4,BO=3,
∴CO=$\sqrt{B{C}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5.
∵AD∥CO,
∴∠COB=∠A,
∵∠D=∠CBO=90°,
∴△CBO∽△BDA,
∴$\frac{BO}{AD}$=$\frac{CO}{AB}$,
∴$\frac{3}{AD}$=$\frac{5}{6}$,
∴AD=$\frac{18}{5}$.
点评 本题考查切线的性质、全等三角形的判定和性质、圆的有关性质,正确寻找相似三角形是解题的关键,记住切线垂直于过切点的半径、直径所对的圆周角是直角,属于中考常考题型.

练习册系列答案
相关题目
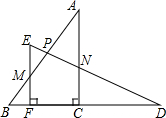 将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.
将两个全等的直角三角板ABC和DEF摆成如图形式,使点B,F,C,D在同一条直线上.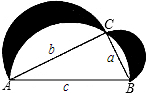 如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.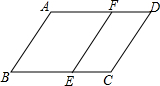 如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?
如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?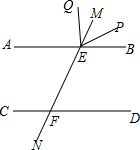 如图所示,已知直线AB,CD被直线MN所截,分别交于E,F,从E点引出两条射线EP,EQ,且满足∠PEQ=∠EFD,∠BEP=∠MEQ,直线AB,CD是否平行?为什么?
如图所示,已知直线AB,CD被直线MN所截,分别交于E,F,从E点引出两条射线EP,EQ,且满足∠PEQ=∠EFD,∠BEP=∠MEQ,直线AB,CD是否平行?为什么?