题目内容
3.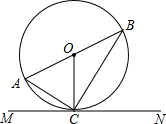 直线MN切⊙O于点C,AB是⊙O的直径且∠CAB=53°,则∠BOC=106°,∠ACB=90°,∠ACM=37°,∠BCN=53°.
直线MN切⊙O于点C,AB是⊙O的直径且∠CAB=53°,则∠BOC=106°,∠ACB=90°,∠ACM=37°,∠BCN=53°.
分析 根据题意可以得到∠OCN=∠OCM=90°,∠ACB=90°,OA=OC、OC=OB,从而可以得到∠BOC的度数,∠ACM、∠BCN的度数,本题得以解决.
解答 解:∵∠CAB=53°,
∴∠COB=2∠CAB=106°,
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠OBC=90°-53°=37°,
∵OA=OC,OC=OB,直线MN切⊙O于点C,
∴∠BAC=∠OCA,∠OCB=∠OBC,∠OCM=∠OCN=90°,
∴∠ACM=∠OCM-∠OCA=90°-53°=37°,∠BCN=∠OCN-∠OCB=90°-37°=53°,
故答案为:106°,90°、37°,53°.
点评 本题考查切线的性质、圆周角与圆心角的关系,解题的关键是明确题意,灵活变化,找出所求问题需要的条件.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
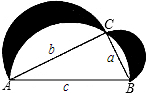 如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
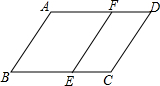 如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?
如图,∠B+∠C=180°,∠A=∠DFE,能得到EF∥CD吗?为什么?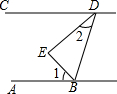 如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.
如图所示,BE是∠ABD的平分线,DE是∠BDC的平分线,且∠1+∠2=90°,那么直线AB,CD的位置关系如何?并说明理由.