ƒøƒ⁄»ð
1£Æ“—÷™µ»±þ°˜ABC∫ÕRt°˜DEF∞¥»ÁÕº1À˘ 浃Œª÷√∑≈÷√£¨µ„B°¢D÷ÿ∫œ£¨«“µ„E°¢B£®D£©°¢C‘⁄Õ¨“ªÃı÷±œþ…œ£Æ∆‰÷–°œDEF=90°„£¨°œEDF=30°„£¨AB=DE=$6\sqrt{3}$£¨œ÷Ω´°˜DEF—ÿ÷±œþBC“‘√ø√Î$\sqrt{3}$∏ˆµ•ŒªœÚ”“∆Ω“∆£¨÷±÷¡Eµ„”ÎCµ„÷ÿ∫œ ±Õ£÷π‘À∂Ø£¨…Ë‘À∂Ø ±º‰Œ™t√ΣÆ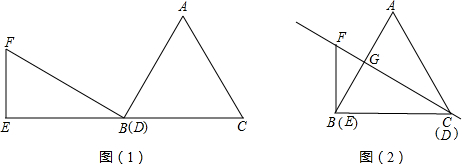
£®1£© ‘«Û≥ˆ‘⁄∆Ω“∆π˝≥Ã÷–£¨µ„F¬‰‘⁄°˜ABCµƒ±þ…œ ±µƒt÷µ£ª
£®2£© ‘«Û≥ˆ‘⁄∆Ω“∆π˝≥Ã÷–°˜ABC∫ÕRt°˜DEF÷ÿµ˛≤ø∑÷µƒ√ʪ˝S”Îtµƒ∫Ø ˝πÿœµ Ω£ª
£®3£©µ±D”ÎC÷ÿ∫œ ±£®»ÁÕº2£©£¨DF”ÎABΩª”⁄Gµ„£¨µ„HŒ™÷±œþDF…œ“ª∂ص„£¨œ÷Ω´°˜BDH»∆µ„DÀ≥ ±’Ζ˝◊™60°„µ√µΩ°˜ACK£¨ «∑ҥʑ⁄µ„H£¨ πµ√°˜ACKŒ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨¡¨Ω”AF£¨≤¢«Û≥ˆ°˜AFKµƒ√ʪ˝£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
∑÷Œˆ £®1£©∑÷µ±F‘⁄±þAB…œ ±∫Õ‘⁄AC±þ…œ ±£¨¡Ω÷÷«ÈøˆΩ¯––Ã÷¬€£¨∑÷±¿˚”√œýÀ∆»˝Ω«–Œµƒ∂‘”¶±þµƒ±»œýµ»«Ûµ√“∆∂صƒæý¿Î£¨º¥ø…«Ûµ√ ±º‰£ª
£®2£©∏˘æð£®1£©µ√µΩµƒ ±º‰£¨º¥ø…∏˘æðtµƒ∑∂Œß∑÷«ÈøˆΩ¯––Ã÷¬€£¨∏˘æðœýÀ∆»˝Ω«–Œµƒ–‘÷ £¨“‘º∞»˝Ω«–Œµƒ√ʪ˝π´ Ωº¥ø…µ√µΩ∫Ø ˝Ω‚Œˆ Ω£ª
£®3£© ◊œ»«Ûµ√µ±B£¨H£¨K‘⁄“ªÃı÷±œþ…œ ±CKµƒ≥§∂»£¨»ª∫Û¿˚”√£∫°˜BHKµƒ√ʪ˝°¢°˜BCKµƒ√ʪ˝°¢°˜XKHµƒ√ʪ˝°¢°˜BCHµƒ√ʪ˝÷ƺ‰µƒπÿœµ£¨º¥ø…µ√µΩ“ª∏ˆπÿ”⁄CKµƒ≥§∂»µƒ∑Ω≥ã¨Ω‚µ√CKµƒ≥§∂»£Æ
Ω‚¥ £®1£©µ±F‘⁄±þAB…œ ±£¨»ÁÕº£®1£©£¨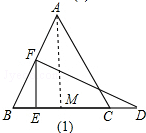
◊˜AM°ÕBC£¨‘ÚAM=$\frac{\sqrt{3}}{2}$AB=$\frac{\sqrt{3}}{2}$°¡6$\sqrt{3}$=9£¨
°þAM°ÕBC£¨°œFEB=90°„
°ýEF°ŒAM£¨
°ý°˜BEF°◊°˜BMA£¨
°ý$\frac{BE}{BM}$=$\frac{EF}{AM}$£¨º¥$\frac{BE}{3\sqrt{3}}$=$\frac{6}{9}$£¨Ω‚µ√£∫BE=2$\sqrt{3}$£¨‘Ú“∆∂صƒæý¿Î «£∫6$\sqrt{3}$+2$\sqrt{3}$=8$\sqrt{3}$£¨‘Út=$\frac{8\sqrt{3}}{\sqrt{3}}$=8£ª
µ±F‘⁄AC…œ ±£¨»ÁÕº£®2£©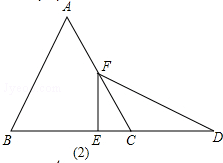
Õ¨¿Ìø…µ√£∫EC=2$\sqrt{3}$£¨‘Ú“∆∂صƒæý¿Î «£∫2°¡6$\sqrt{3}$-2$\sqrt{3}$=12$\sqrt{3}$-2$\sqrt{3}$=10$\sqrt{3}$£¨‘Út=$\frac{10\sqrt{3}}{\sqrt{3}}$=10£¨
π tµƒ÷µ «£∫8ªÚ10£ª
£®2£©µ±0£ºt°Ð6 ±£¨÷ÿ∫œ≤ø∑÷ «»˝Ω«–Œ£¨»ÁÕº£®3£©£¨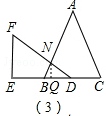
…ËAB”ÎBEΩª”⁄µ„N£¨
‘ÚBD=$\sqrt{3}$t£¨
‘ÚNB=$\frac{1}{2}$BD=$\frac{\sqrt{3}}{2}$t£¨ND=$\frac{\sqrt{3}}{2}$BD=$\frac{\sqrt{3}}{2}$°¡$\sqrt{3}$t=$\frac{\sqrt{3}}{2}$t£¨‘Ús=$\frac{1}{2}$NB°¡ND=$\frac{1}{2}$°¡$\frac{\sqrt{3}}{2}$t°¡$\frac{3}{2}$t=$\frac{3\sqrt{3}}{8}$t2£ª
µ±6£ºt£º10 ±£¨»ÁÕº£®4£©£¨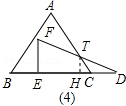
‘ÚCD=$\sqrt{3}$t-6$\sqrt{3}$£¨
°þ°œTCB=60°„£¨°œD=30°„
°ý°œDTC=30°„£¨
°ý°œD=°œDTC£¨
°ýTC=CD=$\sqrt{3}$t-6$\sqrt{3}$£¨
‘Ú‘⁄÷±Ω«°˜THC÷–£¨TH=$\frac{\sqrt{3}}{2}$TC=$\frac{\sqrt{3}}{2}$£®$\sqrt{3}$t-6$\sqrt{3}$£©=$\frac{3}{2}$t-9£¨
‘Ús=18-$\frac{1}{2}$CD°¡TH=18-$\frac{1}{2}$£®$\sqrt{3}$t-6$\sqrt{3}$£©£®$\frac{3}{2}$t-9£©=-$\frac{3\sqrt{3}}{4}$£®t-6£©2+18£ª
µ±10°Ðt£º12 ±£¨÷ÿ∫œ≤ø∑÷»ÁÕº£®5£©£¨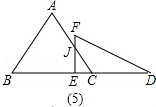
EC=12$\sqrt{3}$-$\sqrt{3}$t£¨
‘Ú÷±Ω«°˜ECJ÷–£¨EJ=$\sqrt{3}$EC=$\sqrt{3}$£®12$\sqrt{3}$-$\sqrt{3}$t£©£¨
‘Ús=$\frac{1}{2}$EC°¡EJ=$\frac{1}{2}$°¡$\sqrt{3}$£®12$\sqrt{3}$-$\sqrt{3}$t£©2=$\frac{3\sqrt{3}}{2}$£®12-t£©2£Æ
£®3£©»ÁÕº£®6£©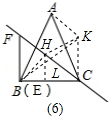
µ±B£¨H£¨K‘⁄“ªÃı÷±œþ…œ ±£¨CH=CK=BC°¡tan30°„=6$\sqrt{3}$°¡$\frac{\sqrt{3}}{3}$=6£¨
…ËCH=x£¨◊˜HL°ÕBC”⁄µ„L£¨‘ÚHL=$\frac{1}{2}$x£¨
°˜CKH «±þ≥§ «xµƒµ»±þ»˝Ω«–Œ£¨‘Ú√ʪ˝ «$\frac{\sqrt{3}}{4}$x2£¨
°˜BCHµƒ√ʪ˝ «£∫$\frac{1}{2}$BC°¡HL=3$\sqrt{3}$°¡$\frac{1}{2}$x=$\frac{3\sqrt{3}}{2}$x£¨
°˜BCKµƒ√ʪ˝ «£∫3$\sqrt{3}$x£Æ
µ±0£ºCH£º6 ±£¨°˜BHKµƒ√ʪ˝=°˜BCKµƒ√ʪ˝-°˜CKHµƒ√ʪ˝-°˜BCHµƒ√ʪ˝£¨
º¥3$\sqrt{3}$x-$\frac{3\sqrt{3}}{2}$x-$\frac{\sqrt{3}}{4}$x2=4$\sqrt{3}$£¨∑Ω≥ÃŒÞΩ‚£Æ
µ±CH£æ6 ±£¨°˜BHKµƒ√ʪ˝=°˜CKHµƒ√ʪ˝+°˜BCHµƒ√ʪ˝-°˜BCKµƒ√ʪ˝£¨
º¥$\frac{\sqrt{3}}{4}$x2+$\frac{3\sqrt{3}}{2}$x-3x$\sqrt{3}$=4$\sqrt{3}$£¨
Ω‚µ√£∫x=8ªÚ-2£®…·»•£©£¨π x=8
°ýCH=8£Æ
µ„∆¿ ¥À «º∏∫Œ±‰ªª◊€∫œÃ‚£¨±æÂøº≤È¡ÀœýÀ∆»˝Ω«–Œµƒ–‘÷ £¨’˝»∑∂‘tµƒ«ÈøˆΩ¯––∑÷¿ý «πÿº¸£Æ

 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏| A£Æ | 20°„ | B£Æ | 50°„ | C£Æ | 70°„ | D£Æ | 130°„ |
| A£Æ | 2∏ˆ | B£Æ | 3∏ˆ | C£Æ | 4∏ˆ | D£Æ | 5∏ˆ |
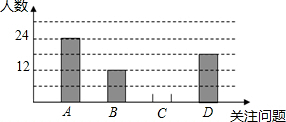 ÀÊ◊≈»À¿ýµƒΩ¯≤Ω£¨»À√«‘Ω¿¥‘Ωπÿ◊¢÷Ќߪ∑æ≥µƒ±‰ªØ£¨…Áª·“≤ª˝º´∫Ù”ı¥Ûº“∂ºŒ™ª∑æ≥æ°∑𡶣Ɩ°√˜ª˝º´—ßœ∞”Ζ˚¥´£¨≤¢¥”Àƒ∏ˆ∑Ω√Ê£∫A-ø’∆¯Œ€»æ£¨B-µ≠ÀÆ◊ ‘¥Œ£ª˙£¨C-Õ¡µÿªƒƒÆªØ£¨D-»´«Ú±‰≈Ø£¨∂‘»´–£Õ¨—ßΩ¯––¡ÀÀʪ˙≥È—˘µ˜≤È£¨¡ÀΩ‚À˚√«‘⁄’‚Àƒ∏ˆ∑Ω√Ê÷–◊Óπÿ◊¢µƒŒ £®√ø»ÀœÞ—°“ªœÓ£©£¨“‘œ¬ «À˚ ’ºØ ˝æð∫Û£¨ªÊ÷∆µƒ≤ªÕÍ’˚µƒÕ≥º∆Õº±Ì∫ÕÕ≥º∆Õº£∫
ÀÊ◊≈»À¿ýµƒΩ¯≤Ω£¨»À√«‘Ω¿¥‘Ωπÿ◊¢÷Ќߪ∑æ≥µƒ±‰ªØ£¨…Áª·“≤ª˝º´∫Ù”ı¥Ûº“∂ºŒ™ª∑æ≥æ°∑𡶣Ɩ°√˜ª˝º´—ßœ∞”Ζ˚¥´£¨≤¢¥”Àƒ∏ˆ∑Ω√Ê£∫A-ø’∆¯Œ€»æ£¨B-µ≠ÀÆ◊ ‘¥Œ£ª˙£¨C-Õ¡µÿªƒƒÆªØ£¨D-»´«Ú±‰≈Ø£¨∂‘»´–£Õ¨—ßΩ¯––¡ÀÀʪ˙≥È—˘µ˜≤È£¨¡ÀΩ‚À˚√«‘⁄’‚Àƒ∏ˆ∑Ω√Ê÷–◊Óπÿ◊¢µƒŒ £®√ø»ÀœÞ—°“ªœÓ£©£¨“‘œ¬ «À˚ ’ºØ ˝æð∫Û£¨ªÊ÷∆µƒ≤ªÕÍ’˚µƒÕ≥º∆Õº±Ì∫ÕÕ≥º∆Õº£∫| πÿ◊¢Œ  | ∆µ ˝ | ∆µ¬ |
| A | 24 | B |
| B | 12 | 0.2 |
| C | N | 0.1 |
| D | 18 | M |
| ∫œº∆ | a | 1 |
£®1£©«Û≥ˆ±Ì÷–◊÷ƒ∏a°¢bµƒ÷µ£¨≤¢Ω´Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®2£©»Áπ˚–°√˜À˘‘⁄µƒ—ß–£”–4000√˚—ß…˙£¨ƒ«√¥∏˘æð–°√˜Ã·π©µƒ–≈œ¢π¿º∆∏√–£πÿ◊¢°∞»´«Ú±‰≈Ø°±µƒ—ß…˙¥Û‘º”–∂ý…Ÿ»À£ø
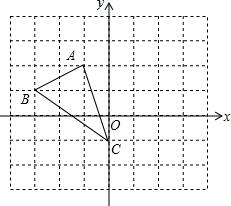 »ÁÕº£¨∑Ω∏Ò÷Ω÷–µƒ√ø∏ˆ–°∑Ω∏Ò∂º «±þ≥§Œ™1∏ˆµ•Œªµƒ’˝∑Ω–Œ£¨‘⁄Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ∫Û£¨°˜ABCµƒ∂•µ„æ˘‘⁄∏Òµ„…œ£¨µ„Cµƒ◊¯±ÍŒ™£®0£¨-1£©£Æ
»ÁÕº£¨∑Ω∏Ò÷Ω÷–µƒ√ø∏ˆ–°∑Ω∏Ò∂º «±þ≥§Œ™1∏ˆµ•Œªµƒ’˝∑Ω–Œ£¨‘⁄Ω®¡¢∆Ω√Ê÷±Ω«◊¯±Íœµ∫Û£¨°˜ABCµƒ∂•µ„æ˘‘⁄∏Òµ„…œ£¨µ„Cµƒ◊¯±ÍŒ™£®0£¨-1£©£Æ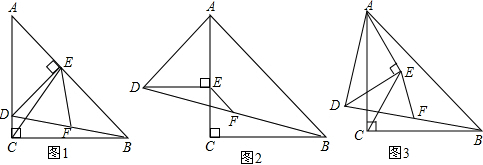
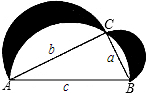 »ÁÕº£¨“—÷™‘⁄°˜ABC÷–£¨°œACB=90°„£¨∑÷±“‘¥À÷±Ω«»˝Ω«–Œµƒ»˝±þŒ™÷±æ∂ª≠∞Α≤£¨ ‘Àµ√˜Õº÷–“ı”∞≤ø∑÷µƒ√ʪ˝”Î÷±Ω«»˝Ω«–Œµƒ√ʪ˝œýµ»£Æ
»ÁÕº£¨“—÷™‘⁄°˜ABC÷–£¨°œACB=90°„£¨∑÷±“‘¥À÷±Ω«»˝Ω«–Œµƒ»˝±þŒ™÷±æ∂ª≠∞Α≤£¨ ‘Àµ√˜Õº÷–“ı”∞≤ø∑÷µƒ√ʪ˝”Î÷±Ω«»˝Ω«–Œµƒ√ʪ˝œýµ»£Æ