题目内容
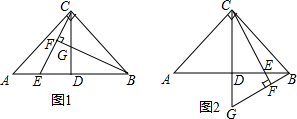
6.如图①,等边△ABC的两边上的点M,N满足BM=AN,BN交CM于点E(1)求证:BM2=ME•MC;
(2)如图②,把△BCE沿着BC向下翻折到△BCF,延长CF和BF交A于P,交AC于K,若等边△ABC的边长是10,求BP•CK的值.
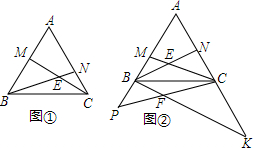
分析 (1)先证明△ABN≌△BCM,再证明△BEM∽△CBM即可.
(2)只要证明△PCB∽△BCK得$\frac{PB}{BC}$=$\frac{BC}{CK}$,由此即可解决问题.
解答 (1)证明:如图①中,∵△ABC是等边三角形,
∴AB=AC,∠A=∠CBM=60°,
在△ABN和△BCM中,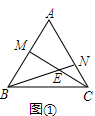
$\left\{\begin{array}{l}{AB=BC}\\{∠A=∠CBM}\\{AN=BM}\end{array}\right.$,
∴△ABN≌△BCM,
∴∠ABN=∠BCM,
又∵∠BME=∠CBM,
∴△BEM∽△CBM,
∴$\frac{BM}{ME}$=$\frac{MC}{BM}$,
即BM2=ME•MC.
(2)解:如图②中,∵△BCF是由△BCE翻折,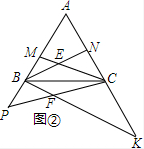
∴∠NBC=∠KBC,∠MCB=∠PCB,
∵∠ABN=∠BCM,
∴∠ABN=∠BCM=∠PCB,
∵∠ABN+∠NBC=60°,∠PCB+∠BPC=60°,
∴∠BPC=∠NBC=∠KBC,
∴△PCB∽△BCK,
∴$\frac{PB}{BC}$=$\frac{BC}{CK}$,
∴PB•CK=BC2=100
点评 本题考查等边三角形的性质、全等三角形的判定和性质、相似三角形的判定和性质等知识,熟练掌握这些判定方法和性质定理,是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
10.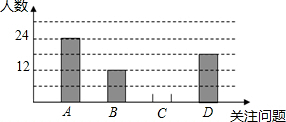 随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:
随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:
根据表中提供的信息解答以下问题:
(1)求出表中字母a、b的值,并将条形统计图补充完整;
(2)如果小明所在的学校有4000名学生,那么根据小明提供的信息估计该校关注“全球变暖”的学生大约有多少人?
 随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:
随着人类的进步,人们越来越关注周围环境的变化,社会也积极呼吁大家都为环境尽份力.小明积极学习与宣传,并从四个方面:A-空气污染,B-淡水资源危机,C-土地荒漠化,D-全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项),以下是他收集数据后,绘制的不完整的统计图表和统计图:| 关注问题 | 频数 | 频率 |
| A | 24 | B |
| B | 12 | 0.2 |
| C | N | 0.1 |
| D | 18 | M |
| 合计 | a | 1 |
(1)求出表中字母a、b的值,并将条形统计图补充完整;
(2)如果小明所在的学校有4000名学生,那么根据小明提供的信息估计该校关注“全球变暖”的学生大约有多少人?
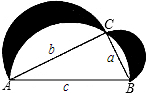 如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
如图,已知在△ABC中,∠ACB=90°,分别以此直角三角形的三边为直径画半圆,试说明图中阴影部分的面积与直角三角形的面积相等.
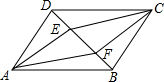 在?ABCD中,BD是对角线,AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AECF是平行四边形.
在?ABCD中,BD是对角线,AE⊥BD,CF⊥BD,E、F为垂足,求证:四边形AECF是平行四边形.