题目内容
6.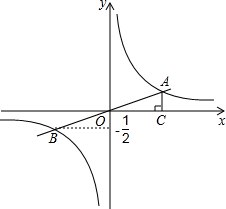 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:(1)反比例函数的函数表达式;
(2)一次函数的函数表达式.
分析 (1)由AC=1,OC=2,且点A在第一象限求出点A的坐标为(2,1),把点A的坐标代入在反比例函数y=$\frac{m}{x}$(m≠0),求得m=2,得到反比例函数的函数表达式:y=$\frac{2}{x}$;
(2)由点B在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,且点B的纵坐标为-$\frac{1}{2}$,
求得点B的横坐标x=-4,得到B(-4,-$\frac{1}{2}$),因为点A,B在一次函数y=kx+b(k≠0)的图象上,代入解析式得到方程组解得即可.
解答 解:(1)∵AC=1,OC=2,且点A在第一象限
∴点A的坐标为(2,1)
∵点A在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,
∴m=2,
∴反比例函数的函数表达式:y=$\frac{2}{x}$;
(2)∵点B在反比例函数y=$\frac{m}{x}$(m≠0)的图象上,且点B的纵坐标为-$\frac{1}{2}$,
∴x=-4,
∴B(-4,-$\frac{1}{2}$),
∵点A,B在一次函数y=kx+b(k≠0)的图象上,
∴$\left\{\begin{array}{l}{1=2k+b}\\{-\frac{1}{2}=-4k+b}\end{array}\right.$,∴$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=\frac{1}{2}}\end{array}\right.$,
∴一次函数的函数表达式:y=$\frac{1}{4}$x+$\frac{1}{2}$.
点评 本题考查了利用函数的解析式求点的坐标,待定系数法求函数的解析式,用待定系数法确定函数的解析式,是常用的一种解题方法.同学们要熟练掌握这种方法.

练习册系列答案
相关题目
 如图,在△ABC中,D为BC边上一点,∠B=∠C=∠BAD=36°
如图,在△ABC中,D为BC边上一点,∠B=∠C=∠BAD=36° 如图,在△ABC中,∠CBA=60°,∠BAC=72°,D在BC上一点,DE交AC于点F,且AB=AD=DE.连接AE,∠E=55°,请判断△AFD的形状,并说明理由.
如图,在△ABC中,∠CBA=60°,∠BAC=72°,D在BC上一点,DE交AC于点F,且AB=AD=DE.连接AE,∠E=55°,请判断△AFD的形状,并说明理由. 如图,在△ABC中,AB=AC=10,BC=16,AD⊥AC交BC于D,求DB的长.
如图,在△ABC中,AB=AC=10,BC=16,AD⊥AC交BC于D,求DB的长. 如图,在平行平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,求平行四边形ABCD的周长.
如图,在平行平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,求平行四边形ABCD的周长.