题目内容
1.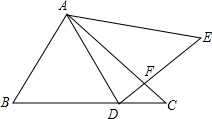 如图,在△ABC中,∠CBA=60°,∠BAC=72°,D在BC上一点,DE交AC于点F,且AB=AD=DE.连接AE,∠E=55°,请判断△AFD的形状,并说明理由.
如图,在△ABC中,∠CBA=60°,∠BAC=72°,D在BC上一点,DE交AC于点F,且AB=AD=DE.连接AE,∠E=55°,请判断△AFD的形状,并说明理由.
分析 先根据等腰三角形的性质得出∠ADB=∠B,再由三角形内角和定理求出∠BAD的度数,进而得出∠DAC的度数.再根据AD=DE得出∠DAE=∠E,由三角形内角和定理求出∠ADE的度数,再求出∠AFD的度数,进而得出结论.
解答 解:△AFD是钝角三角形.
理由如下:
∵AB=AD,
∴∠ADB=∠B=60°
∴∠BAD=180°-2×60°=60°,∠DAC=72°-60°=12°.
∵AD=DE,
∴∠DAE=∠E=55°,∠ADE=180°-2×55°=70°,
∴∠AFD=180°-∠DAE-∠ADE=180°-12°-70°=98°,
∴△AFD是钝角三角形.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
相关题目
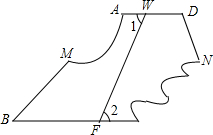 如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数.
如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数.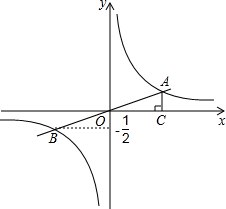 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求: