题目内容
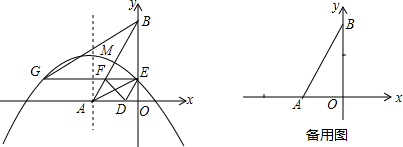
16. 如图,在△ABC中,D为BC边上一点,∠B=∠C=∠BAD=36°
如图,在△ABC中,D为BC边上一点,∠B=∠C=∠BAD=36°(1)若BC=1,求AB的值;
(2)求tan236°.
分析 (1)先证出△ABD∽△ABC,得出$\frac{AB}{CB}$=$\frac{BD}{AB}$,再根据AB•AB=1(1-AB)进行整理即可得出AB;
(2)过点A作AM⊥BC,设BC=1,则CM=$\frac{1}{2}$,根据AC=$\frac{\sqrt{5}-1}{2}$求出AM2,再根据tan236°=tan2∠B=($\frac{AM}{CM}$)2代入计算即可.
解答 解:(1)∵∠B=∠C=∠BAD=36°,
∴AB=AC,BD=AD,
∴∠CDA=∠CAD=72°,
∴AC=CD,
∴△ABD∽△ABC,
∴$\frac{AB}{CB}$=$\frac{BD}{AB}$,
∴AB•AB=1(1-AB),
∴AB=$\frac{\sqrt{5}-1}{2}$;
(2)过点A作AM⊥BC,设BC=1,则CM=$\frac{1}{2}$,
∵AC=AB=$\frac{\sqrt{5}-1}{2}$;
∴AM2=AC2-CM2=($\frac{\sqrt{5}-1}{2}$)2-($\frac{1}{2}$)2=$\frac{5-2\sqrt{5}}{4}$,
∴tan236°=tan2∠B=($\frac{AM}{CM}$)2=$\frac{A{M}^{2}}{C{M}^{2}}$=$\frac{\frac{5-2\sqrt{5}}{4}}{(\frac{1}{2})^{2}}$=5-2$\sqrt{5}$.
点评 此题考查了黄金分割,用到的知识点是黄金分割的定义、相似三角形的判定与性质、等腰三角形的性质、正切的定义,关键是根据题意画出图形,构造直角三角形.

练习册系列答案
相关题目
7.下列运算正确的是( )
| A. | $\sqrt{4}$=2 | B. | (-3)2=-9 | C. | 2-3=-6 | D. | 20=0 |
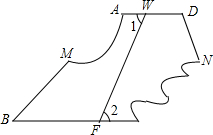 如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数.
如图是一张四边形纸片ABCD被撕掉∠A和∠C后的剩余部分(∠A在左上角),量得∠1=∠2,∠B=45°,∠D=105°,在图中画出被撕掉的部分,并求原来∠A和∠C的度数.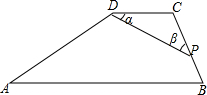 如图,四边形ABCD中,AB∥CD,P为BC上一点,设∠CDP=∠α,∠CPD=∠β,当P在BC上移动时,总有∠α+∠β=∠B成立?请你利用你学过的数学知识说明理由.
如图,四边形ABCD中,AB∥CD,P为BC上一点,设∠CDP=∠α,∠CPD=∠β,当P在BC上移动时,总有∠α+∠β=∠B成立?请你利用你学过的数学知识说明理由. 如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.
如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.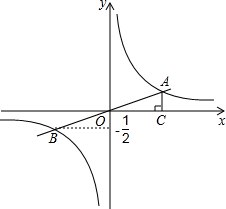 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求: