题目内容
18. 如图,在△ABC中,AB=AC=10,BC=16,AD⊥AC交BC于D,求DB的长.
如图,在△ABC中,AB=AC=10,BC=16,AD⊥AC交BC于D,求DB的长.
分析 先根据勾股定理求出AE=6,设BD=x,则DE=8-x,DC=16-x,在Rt△ADE和Rt△ADC中利用勾股定理得:AD2=AE2+DE2=DC2-AC2,继而代入求出x的值即可.
解答  解:过点A作AE⊥BC与点E,
解:过点A作AE⊥BC与点E,
∵AB=AC=10,BC=16,
∴BE=CE=8,
在Rt△ACE中,利用勾股定理可知:AE=$\sqrt{{AC}^{2}-{CE}^{2}}$=$\sqrt{{10}^{2}-{8}^{2}}$=6,
设BD=x,则DE=8-x,DC=16-x,
又因为DA⊥CA,
在Rt△ADE和Rt△ADC中分别利用勾股定理得:AD2=AE2+DE2=DC2-AC2,
代入为:62+(8-x)2=(16-x)2-102,解得:x=$\frac{7}{2}$,即DB=$\frac{7}{2}$.
点评 本题考查勾股定理及等腰三角形的性质,解题关键是在Rt△ADE和Rt△ADC中分别利用勾股定理,列出等式AD2=AE2+DE2=DC2-AC2.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
7.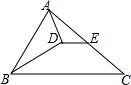 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )| A. | ∠BAD=∠C+∠DAE | B. | DE∥BC | C. | DE=$\frac{1}{2}(BC-AB)$ | D. | BD=EC |
 如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.
如图,O为矩形ABCD内的一点,且满足OB=OD,若O点到A点的距离用m表示,OB=n,试用含m、n的代数式表示OC=$\sqrt{2{n}^{2}-{m}^{2}}$.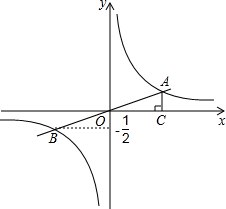 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求: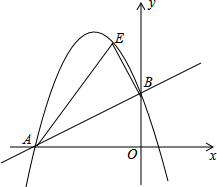 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE.