题目内容
16. 如图,在平行平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,求平行四边形ABCD的周长.
如图,在平行平行四边形ABCD中,DE平分∠ADC,AD=6,BE=2,求平行四边形ABCD的周长.
分析 根据平行四边形的性质得出AB=CD,AD=BC=6,AD∥BC,根据平行线性质求出∠ADE=∠DEC,根据角平分线定义求出∠ADE=∠CDE,推出∠CDE=∠DEC,推出CE=DC,求出CD、即可求出答案.
解答 解:∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC=6,AD∥BC,
∴∠ADE=∠DEC,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠CDE=∠DEC,
∴CE=DC,
∵BC=6,BE=2,
∴CD=CE=6-2=4,
∴AB=CD=4,
∴平行四边形ABCD的周长为AD+CD+BC+AB=6+4+6+4=20.
点评 本题考查了平行四边形的性质,角平分线定义,平行线的性质,等腰三角形的性质和判定的应用,解此题的关键是求出CD的长,注意:平行四边形的对边平行且相等,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.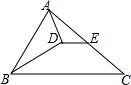 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )| A. | ∠BAD=∠C+∠DAE | B. | DE∥BC | C. | DE=$\frac{1}{2}(BC-AB)$ | D. | BD=EC |
20. 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{\sqrt{41}}{2}$ |
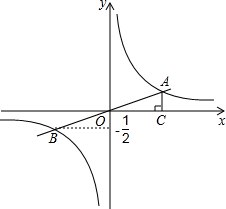 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求: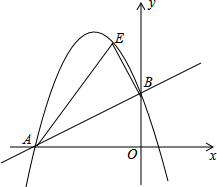 如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE.
如图,在平面直角坐标系中,直线y=$\frac{1}{2}$x+2与坐标轴分别交于A、B两点,过A、B两点的抛物线为y=-x2+bx+c,点E为第二象限内抛物线上一动点,连接AE,BE.