题目内容
15.已知一个三角形有两边相等,并且周长为56cm,两不等边之比为3:2,求这个三角形各边的长.分析 可以设三角形的边长为a、a、b,根据周长和两不等边之比为3:2可以得到两个方程组,注意要分两种情况讨论,a:b=3:2时或b:a=3:2时看结果是否符合三角形三边关系.
解答 解:设三角形的边长为a、a、b,根据题意有如下两种情况:
$\left\{\begin{array}{l}{a+a+b=56}\\{a:b=3:2}\end{array}\right.$①或$\left\{\begin{array}{l}{a+a+b=56}\\{b:a=3:2}\end{array}\right.$②,
由①解得:$\left\{\begin{array}{l}{b=14}\\{a=21}\end{array}\right.$,
由②解得:$\left\{\begin{array}{l}{a=16}\\{b=24}\end{array}\right.$,
∵a+b=14+21=35>21,2a=32>24,∴此两组解符合题意.
故这个三角形的三边长分别是21、21、14或16、16、24.
点评 此题考查三角形问题,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.本题要注意分情况讨论并结合三角形三边关系确定其边长,属于一道小型综合题.

练习册系列答案
相关题目
7.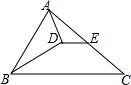 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
 如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )
如图,在△ABC中,BD是∠ABC的角平分线,AD⊥BD于D,E是AC的中点,下列结论中不正确的是( )| A. | ∠BAD=∠C+∠DAE | B. | DE∥BC | C. | DE=$\frac{1}{2}(BC-AB)$ | D. | BD=EC |
20. 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
 如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )
如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为( )| A. | $\frac{7}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | 2$\sqrt{3}$ | D. | $\frac{\sqrt{41}}{2}$ |
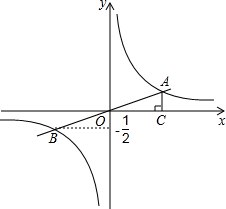 如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求:
如图,一次函数y=kx+b(k≠0)的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象相交于点A、B,且点B的纵坐标为-$\frac{1}{2}$,过点A作AC⊥x轴,垂足为C,AC=1,OC=2.求: