题目内容
12.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.(1)如图(1),当直线l与⊙O相切于点C时,若∠DAC=35°,求∠DAB的度数;
(2)如图(2),当直线l与⊙O相交于点E、F时,求证:∠DAE=∠BAF.

分析 (1)连接OC,如图1,根据切线的性质得OC⊥l,加上AD⊥l,则AD∥OC,所以∠OCA=∠DAC=35°,由于∠OAC=∠OCA=35°,易得∠DAB=70°;
(2)连结BF,如图2,先根据圆周角定理得到∠AFB=90°,再根据圆内接四边形的性质得∠AED=∠ABF,然后利用等角的余角相等即可得到结论.
解答 (1)解:连接OC,如图1,
∵直线l与⊙O相切于点C,
∴OC⊥l,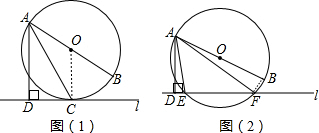
∵AD⊥l,
∴AD∥OC,
∴∠OCA=∠DAC=35°,
∵OA=OC,
∴∠OAC=∠OCA=35°,
∴∠DAB=∠DAC+∠OAC=35°+35°=70°;
(2)证明:连结BF,如图2,
∵AB是⊙O的直径,
∴∠AFB=90°,
∵AD⊥EF,
∴∠ADE=90°,
∵∠AED=∠ABF,
∴∠DAE=∠BAF.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
3. 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
 如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )
如图,一个直角三角板ABC绕其直角顶点C旋转到△DCE的位置,若∠BCD=30°,下列结论错误的是( )| A. | ∠ACD=120° | B. | ∠ACD=∠BCE | C. | ∠ACE=120° | D. | ∠ACE-∠BCD=120° |
17.书店、学校、食堂在平面上分别用A、B、C来表示,书店在学校的北偏西30°,食堂在学校的南偏东15°,则平面图上的∠ABC的度数应该是( )
| A. | 65° | B. | 35° | C. | 165° | D. | 135° |
4. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18. 如图,将Rt△ABC(∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
 如图,将Rt△ABC(∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C,A,B1在同一条直线上,那么旋转角等于( )| A. | 55° | B. | 70° | C. | 125° | D. | 145° |

 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC. 如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交AB边于点F,连接AE交CF于点O,给出下列命题:
如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交AB边于点F,连接AE交CF于点O,给出下列命题: