题目内容
20. 如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.
如图,在平面直角坐标系xOy中,正比例函数y=2x与反比例函数y=$\frac{k}{x}$的图象交于A,B两点,点A的横坐标为2,AC⊥x轴于点C,连接BC.(1)求反比例函数的表达式;
(2)若点P是反比例函数y=$\frac{k}{x}$图象上的一点,且满足△OPC的面积是△ABC面积的一半,请直接写出点P的坐标.
分析 (1)先通过正比例函数求得A的坐标,然后代入y=$\frac{k}{x}$,根据待定系数法即可求得;
(2)由条件可求得B的坐标,根据△ACO的面积是△ABC的面积的$\frac{1}{2}$,即可求得P和A或B重合,从而求得P的坐标.
解答 解:(1)将x=2代入y=2x中,得y=2×2=4.
∴点A坐标为(2,4).
∵点A在反比例函数$y=\frac{k}{x}$的图象上,
∴k=2×4=8.
∴反比例函数的表达式为$y=\frac{8}{x}$.
(2)∵A、B关于原点对称,
∴B点坐标为(-2,-4),
∵S△ABC=2S△ACO,△OPC的面积是△ABC面积的一半,
∴P(2,4)或(-2,-4).
点评 本题主要考查待定系数法求函数解析式及函数的交点问题,求得A点坐标是解题的关键.

练习册系列答案
相关题目
11.如果一次函数y=kx+b,当-3≤x≤1时,-1≤y≤7,则kb的值为( )
| A. | 10 | B. | 21 | C. | -10或2 | D. | -2或10 |
8.直线y=-x+2与x轴交于点A,与y轴交于点B,O是原点,点P是线段AB上的动点(包括A、B两点),以OP为直径作⊙Q,则⊙Q的面积不可能是( )
| A. | 1.5π | B. | π | C. | $\frac{3}{4}$π | D. | $\frac{1}{2}$π |
 如图,在梯形ABCD中,AD∥BC,AC平分∠BCD,∠BAC=∠D,若AD=4,BC=10,则AC=2$\sqrt{10}$.
如图,在梯形ABCD中,AD∥BC,AC平分∠BCD,∠BAC=∠D,若AD=4,BC=10,则AC=2$\sqrt{10}$.
 如图,点C、D分别为线段AB(端点A、B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于40cm,且AD=3CD,则CD=3cm.
如图,点C、D分别为线段AB(端点A、B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于40cm,且AD=3CD,则CD=3cm.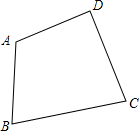 作图题:如图,西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树,要求杏树的位置点P到边AB,BC的距离相等并且点P到A,D的距离也相等,请用尺规作图作出杏树的位置点P(用尺规作图法,保留作图痕迹,不写作法).
作图题:如图,西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树,要求杏树的位置点P到边AB,BC的距离相等并且点P到A,D的距离也相等,请用尺规作图作出杏树的位置点P(用尺规作图法,保留作图痕迹,不写作法).