题目内容
4. 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③9a-3b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:∵抛物线开口向下,
∴a<0,
∵-$\frac{b}{2a}$=-2,
∴b=4a,ab>0,
∴b-4a=0,
∴①错误,④正确,
∵抛物线与x轴交于-4,0处两点,
∴b2-4ac>0,方程ax2+bx=0的两个根为x1=0,x2=-4,
∴②⑤正确,
∵当x=-3时y>0,即9a-3b+c>0,
∴③正确,
故正确的有②③④⑤.
故选:C.
点评 本题主要考查图象与二次函数系数之间的关系,会利用对称轴的范围求2a与b的关系,以及二次函数与方程之间的转换,根的判别式以及特殊值的熟练运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
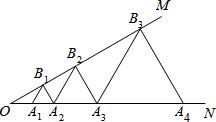 如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=$\frac{1}{3}$,则△A2015B2015A2016的边长为$\frac{{2}^{2014}}{3}$.
如图,已知∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4 …均为等边三角形,若OA1=$\frac{1}{3}$,则△A2015B2015A2016的边长为$\frac{{2}^{2014}}{3}$.
 如图,AB=16cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度.
如图,AB=16cm,延长AB到C,使BC=3AB,D是BC的中点,求AD的长度. 如图,点C、D分别为线段AB(端点A、B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于40cm,且AD=3CD,则CD=3cm.
如图,点C、D分别为线段AB(端点A、B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于40cm,且AD=3CD,则CD=3cm. 某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.
某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示. 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.