题目内容
1.把下列各式分解因式:(1)m(x+y)+n(x+y)-x-y=(x+y)(m+n-1);
(2)x(a-b)2+y(b-a)3=(a-b)2(x-ab+by);
(3)x(m-x)(m-y)-m(m-x)(m-y)=-(m-x)2(m-y);
(4)1+x+x(1+x)+x(1+x)2+x(1+x)3=(1+x)4.
分析 (1)直接提取公因式(x+y),进而分解因式即可;
(2)直接提取公因式(a-b)2,进而分解因式即可;
(3)直接提取公因式(m-x)(m-y),进而分解因式即可;
(4)分别提取公因式(1+x),进而分解因式得出答案.
解答 解:(1)m(x+y)+n(x+y)-x-y=(x+y)(m+n-1).
故答案为:(x+y)(m+n-1);
(2)x(a-b)2+y(b-a)3=(a-b)2(x-ab+by);
故答案为:(a-b)2(x-ab+by);
(3)x(m-x)(m-y)-m(m-x)(m-y)
=(m-x)(m-y)(x-m)
=-(m-x)2(m-y).
故答案为:-(m-x)2(m-y);
(4)1+x+x(1+x)+x(1+x)2+x(1+x)3
=(1+x)[1+x+x(1+x)+x(1+x)2]
=(1+x)2[1+x+x(1+x)]
=(1+x)4.
故答案为:(1+x)4.
点评 此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
11.如果一次函数y=kx+b,当-3≤x≤1时,-1≤y≤7,则kb的值为( )
| A. | 10 | B. | 21 | C. | -10或2 | D. | -2或10 |
7. 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
 小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.
小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
| A. | 角的内部到角的两边的距离相等的点在角的平分线上 | |
| B. | 角平分线上的点到这个角两边的距离相等 | |
| C. | 三角形三条角平分线的交点到三条边的距离相等 | |
| D. | 以上均不正确 |

 如图,点C、D分别为线段AB(端点A、B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于40cm,且AD=3CD,则CD=3cm.
如图,点C、D分别为线段AB(端点A、B除外)上的两个不同的动点,点D始终在点C右侧,图中所有线段的和等于40cm,且AD=3CD,则CD=3cm. 某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.
某供电公司,为了鼓励居民用电,采用分段计费的方法来计算电费,月用电x(度)与相应电费y(元)之间的函数的图象如图所示.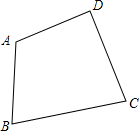 作图题:如图,西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树,要求杏树的位置点P到边AB,BC的距离相等并且点P到A,D的距离也相等,请用尺规作图作出杏树的位置点P(用尺规作图法,保留作图痕迹,不写作法).
作图题:如图,西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树,要求杏树的位置点P到边AB,BC的距离相等并且点P到A,D的距离也相等,请用尺规作图作出杏树的位置点P(用尺规作图法,保留作图痕迹,不写作法).