题目内容
18．
如图，将Rt△ABC（∠B=35°，∠C=90°）绕点A按顺时针方向旋转到△AB1C1的位置，使得点C，A，B1在同一条直线上，那么旋转角等于（ ）| A． | 55° | B． | 70° | C． | 125° | D． | 145° |
分析 首先根据三角形的内角和定理，求出∠BAC的度数是多少；然后根据对应点与旋转中心所连线段的夹角等于旋转角，可得旋转角的度数等于∠BAB1的度数，据此解答即可．
解答 解：∵∠B=35°，∠C=90°，
∴∠BAC=180°-35°-90°=55°，
∵点C，A，B1在同一条直线上，
∴∠BAB1=180°-∠BAC=180°-55°=125°，
即旋转角等于125°．
故选：C．
点评 此题主要考查了旋转的性质和应用，要熟练掌握，解答此题的关键是要明确：①对应点到旋转中心的距离相等．②对应点与旋转中心所连线段的夹角等于旋转角．③旋转前、后的图形全等．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
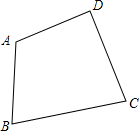作图题：如图，西宁市沈那中学准备在校内一块四边形草坪内栽上一棵杏树，要求杏树的位置点P到边AB，BC的距离相等并且点P到A，D的距离也相等，请用尺规作图作出杏树的位置点P（用尺规作图法，保留作图痕迹，不写作法）．
如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，下面四个结论正确的有（ ）个．
如图，在Rt△ABC中，∠ACB=90°，以AC为直径的⊙O与AB边交于点D，过点D作⊙O的切线，交BC于点E．
7．
小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．
如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）
小明同学在学习了全等三角形的相关知识后发现，只用两把完全相同的长方形直尺就可以作出一个角的平分线．如图：一把直尺压住射线OB，另一把直尺压住射线OA并且与第一把直尺交于点P，小明说：“射线OP就是∠BOA的角平分线．”他这样做的依据是（ ）
| A． | 角的内部到角的两边的距离相等的点在角的平分线上 | |
| B． | 角平分线上的点到这个角两边的距离相等 | |
| C． | 三角形三条角平分线的交点到三条边的距离相等 | |
| D． | 以上均不正确 |