题目内容
17.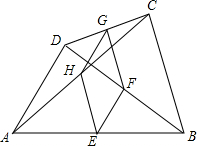 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.①要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是AD=BC;
②要使四边形EFGH是矩形,四边形ABCD还应满足的一个条件是AD⊥BC.
分析 ①由已知条件得出GH是△ADC的中位线,EF是△ABD的中位线,GF是△CBD的中位线,由三角形中位线定理得出GH∥EF,GH=EF,再证出GE=EH,即可得出结论.
②由①得出四边形EFGH是平行四边形,由AD⊥BC,得出GH⊥GF,即可得出结论.
解答 解:①AD=BC;理由如下:
∵点E、F、G、H分别是AB、CD、AC、BD的中点,
∴GH是△ADC的中位线,EF是△ABD的中位线,GF是△CBD的中位线,
∴GH∥AD,GH=$\frac{1}{2}$AD,EF=$\frac{1}{2}$AD,EF∥AD,GF=$\frac{1}{2}$BC,GF∥BC,
∴GH∥EF,GH=EF,
∴四边形EFGH是平行四边形,
又∵AD=BC,
∴GH=GF,
∴四边形EFGH是菱形;
故答案为:AD=BC.
②AD⊥BC,理由如下:由①得:GH∥AD,GH=$\frac{1}{2}$AD,EF=$\frac{1}{2}$AD,EF∥AD,GF=$\frac{1}{2}$BC,GF∥BC,
∴GH∥EF,GH=EF,
∴四边形EFGH是平行四边形,
又∵AD⊥BC,
∴GH⊥GF,
∴四边形EFGH是矩形;
故答案为:AD⊥BC.
点评 本题考查了三角形中位线定理、平行四边形的判定、菱形的判定方法以及矩形的判定;熟练掌握菱形和矩形的判定方法,由三角形中位线定理得出线段之间的关系是解决问题的关键.

练习册系列答案
相关题目
5.下列方程组中,是二元一次方程组的为( )
| A. | $\left\{\begin{array}{l}{x+y=1}\\{x-z=2}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{{y}^{2}-1=0}\\{x-2y=0}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{y-2x=1}\\{y=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{1}{x}+3y=0}\\{x-y=1}\end{array}\right.$ |
 如图,四边形ABCD向右平移一段距离后得到四边形A′B′C′D′.
如图,四边形ABCD向右平移一段距离后得到四边形A′B′C′D′.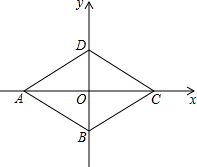 如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(-3,0)、B(0,-1)、C(3,0)、D(0,1).求证:四边形ABCD是菱形.
如图,在平面直角坐标系中,四边形ABCD的顶点坐标分别为A(-3,0)、B(0,-1)、C(3,0)、D(0,1).求证:四边形ABCD是菱形. 如图所示,在矩形ABCD中,AC、BD相交于点O,作OE∥AD,交CD与点F,且OF=FE.
如图所示,在矩形ABCD中,AC、BD相交于点O,作OE∥AD,交CD与点F,且OF=FE. 如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2.
如图,平行四边形ABCD中,∠A的平分线AE交CD于E,AB=5,BC=3,则EC的长为2. 已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是$\frac{50}{13}$、5或$\frac{13}{2}$.
已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是$\frac{50}{13}$、5或$\frac{13}{2}$.