题目内容
9.在平行四边形ABCD中,AC=AB=3,过点A作AE⊥BC,垂足为点E,过点A作AF⊥直线CD,垂足为F,CF=1,则AD的长为2$\sqrt{3}$或2$\sqrt{6}$.分析 分两种情形:①如图1中,当点F在线段CD上时,②如图2中,当点F在DC的延长线上时,分别利用勾股定理计算即可解决问题.
解答 解:①如图1中,当点F在线段CD上时,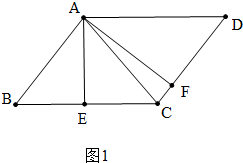
在RT△ACF中,∵∠AFC=90°,AC=3,CF=1,
∴AF2=AC2-CF2=32-12=8,
∵四边形ABCD是平行四边形,
∴CD=AB=3,DF=CD-CF=2,
在RT△ADF中,∵∠AFD=90°,
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{8+{2}^{2}}$=2$\sqrt{3}$.
②如图2中,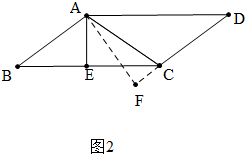
当点F在DC的延长线上时,在RT△ADF中,AF2=8,DF=1+3=4,
∴AD=$\sqrt{A{F}^{2}+D{F}^{2}}$=$\sqrt{8+16}$=2$\sqrt{6}$.
故答案为2$\sqrt{3}$或2$\sqrt{6}$
点评 本题考查平行四边形的性质、勾股定理等知识,解题的关键是熟练运用勾股定理,注意有两种情形不能漏解,考虑问题要全面,属于中考常考题型.

练习册系列答案
相关题目
19.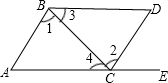 如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
 如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )
如下图所示,点E在AC的延长线上,下列条件中不能判断BD∥AC( )| A. | ∠3=∠4 | B. | ∠1=∠2 | C. | ∠D=∠DCE | D. | ∠D+∠ACD=180° |
4.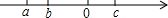 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
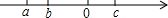 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )| A. | a-2b | B. | 2b+c | C. | -2a+c | D. | a-2b+c |
1. 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )| A. | 1和4 | B. | 4和1 | C. | 2和3 | D. | 3和2 |
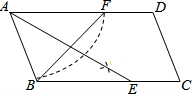 如图,?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为8.
如图,?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为8.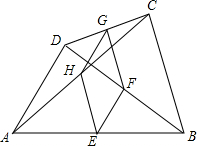 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.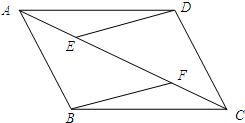 如图,在?ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,BF,求证:DE∥BF.
如图,在?ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,BF,求证:DE∥BF.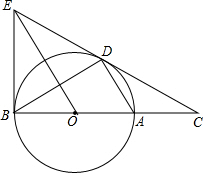 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.