题目内容
7.用换元法解下列方程组:(1)$\left\{\begin{array}{l}{3(x+y)+2(x-y)=36}\\{(x+y)-4(x-y)=-16}\end{array}\right.$
(2)$\left\{\begin{array}{l}{\frac{x-4y}{2}+\frac{x+5y}{3}=2}\\{\frac{x-4y}{3}-(x+5y)=5}\end{array}\right.$.
分析 (1)令x+y=m、x-y=n得关于m、n的方程组,解得m、n的值,从而可得关于x、y的方程组,求解可得;
(2)令x-4y=a、x+5y=b得关于a、b的方程组,解该方程组可得a、b的值,从而可得关于x、y的方程组,求解可得,.
解答 解:(1)令x+y=m,x-y=n,
则原方程组可化为:$\left\{\begin{array}{l}{3m+2n=36}\\{m-4n=-16}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=8}\\{n=6}\end{array}\right.$,
即$\left\{\begin{array}{l}{x+y=8}\\{x-y=6}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=7}\\{y=1}\end{array}\right.$;
(2)令x-4y=a,x+5y=b,
则原方程组可化为:$\left\{\begin{array}{l}{\frac{a}{2}+\frac{b}{3}=2}\\{\frac{a}{3}-b=5}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=6}\\{b=-3}\end{array}\right.$,
即:$\left\{\begin{array}{l}{x-4y=6}\\{x+5y=-3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=2}\\{y=-1}\end{array}\right.$.
点评 本题主要考查换元法解方程组的能力,熟练而准确的解方程组是基础,正确找到共同的整体加以换元是关键.

 名校课堂系列答案
名校课堂系列答案(1)在同一平面内,不相交的两条直线平行;(2)实数于数轴上的点一一对应;
(3)相等的角是对顶角;(4)两条直线被第三条直线所截,所得到同位角相等;
(5)x轴上的点必是纵坐标为0,横坐标不为0;(6)坐标原点不属于任何象限.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
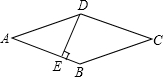 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.8 |
| A. | a2=(m-1)2,b2=4m2,c2=(m+1)2 | B. | a2=(m-1)2,b2=4m,c2=(m+1)2 | ||
| C. | a2=(m-1)2,b2=2m,c2=(m+1)2 | D. | a2=(m-1)2,b2=2m2,c2=(m+1)2 |
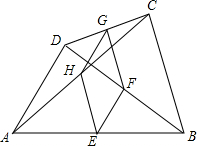 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
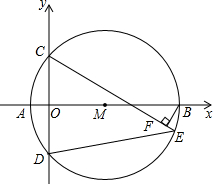 已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.
已知关于x的方程x2+(2m-6)x+m2-7=0有两个不相等的实数根,两根的平方和为10,且两根分别是A点和B点的横坐标(如图),以AB为直径作圆M交y轴于点C和点D,点E是$\widehat{BD}$上一点,BF⊥CE于点F,连接DE.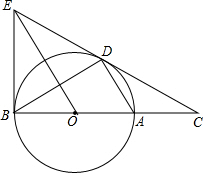 如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.
如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.