题目内容
6. 已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是$\frac{50}{13}$、5或$\frac{13}{2}$.
已知:如图,Rt△ABC中,∠BAC=90°,AB=5,AC=12,将△ABC沿射线BC方向平移m个单位长度到△DEF,顶点A、B、C分别与D、E、F对应,若以点A、D、E为顶点的三角形是等腰三角形,则m的值是$\frac{50}{13}$、5或$\frac{13}{2}$.
分析 过点A作AM⊥BC于点M,过点E作EN⊥AB于点N,由“Rt△ABC中,∠BAC=90°,AB=5,AC=12”可得出∠B的正余弦值.将△ADE为等腰三角形分三种情况考虑,结合等腰三角形的性质以及解直角三角形可分别求出三种情况下BE的长度,由m=BE即可得出结论.
解答 解:过点A作AM⊥BC于点M,过点E作EN⊥AB于点N,如图所示.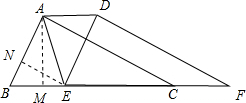
在Rt△ABC中,∠BAC=90°,AB=5,AC=12,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=13,sin∠B=$\frac{AC}{BC}$=$\frac{12}{13}$,cos∠B=$\frac{AB}{BC}$=$\frac{5}{13}$.
△ADE为等腰三角形分三种情况:
①当AB=AE时,
BE=2BM,BM=AB•cos∠B=$\frac{25}{13}$,
此时m=BE=$\frac{50}{13}$;
②当AB=BE时,
m=BE=AB=5;
③当BE=AE时,
BN=AN=$\frac{1}{2}$AB=$\frac{5}{2}$,BE=$\frac{BN}{cos∠B}$=$\frac{13}{2}$,
此时m=BE=$\frac{13}{2}$.
故答案为:$\frac{50}{13}$、5或$\frac{13}{2}$.
点评 本题考查了等腰三角形的性质、勾股定理、平移的性质以及解直角三角形,解题的关键是分三种情况求出BE的长处.本题属于基础题,难度不大,但在解决该题时,部分同学会落掉两种情况,故在解决该题型题目时,全面考虑等腰三角形的三种情况是关键.

练习册系列答案
相关题目
1. 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )| A. | 1和4 | B. | 4和1 | C. | 2和3 | D. | 3和2 |
18.下列说法中正确的个数有( )
(1)在同一平面内,不相交的两条直线平行;(2)实数于数轴上的点一一对应;
(3)相等的角是对顶角;(4)两条直线被第三条直线所截,所得到同位角相等;
(5)x轴上的点必是纵坐标为0,横坐标不为0;(6)坐标原点不属于任何象限.
(1)在同一平面内,不相交的两条直线平行;(2)实数于数轴上的点一一对应;
(3)相等的角是对顶角;(4)两条直线被第三条直线所截,所得到同位角相等;
(5)x轴上的点必是纵坐标为0,横坐标不为0;(6)坐标原点不属于任何象限.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.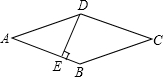 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
 如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )
如图,菱形ABCD的周长为8cm,DE⊥AB,垂足为E,若sinA=$\frac{4}{5}$,则EB的长为( )| A. | 0.4 | B. | 0.5 | C. | 0.6 | D. | 0.8 |
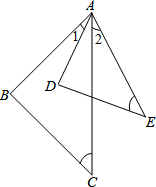 如图,△ABC与△ADE中,∠C=∠E,∠1=∠2;
如图,△ABC与△ADE中,∠C=∠E,∠1=∠2;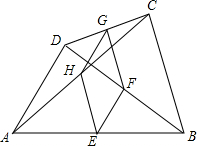 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.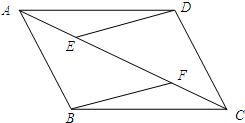 如图,在?ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,BF,求证:DE∥BF.
如图,在?ABCD中,E,F为对角线AC上的两点,且AE=CF,连接DE,BF,求证:DE∥BF.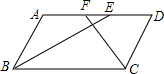 如图,在?ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,AB=3,AD=5,则EF的长为1.
如图,在?ABCD中,BE平分∠ABC交AD于点E,CF平分∠BCD交AD于点F,AB=3,AD=5,则EF的长为1.