题目内容
12. 如图所示,在矩形ABCD中,AC、BD相交于点O,作OE∥AD,交CD与点F,且OF=FE.
如图所示,在矩形ABCD中,AC、BD相交于点O,作OE∥AD,交CD与点F,且OF=FE.求证:四边形OCED是菱形.
分析 根据矩形的性质以及平行线分线段成比例定理,证明四边形OCED的对角线互相平分并且互相垂直,即可证得.
解答 证明:∵矩形ABCD中,AD∥BC,OB=OD,CD⊥AD,
∴DF=FC,
∵CD⊥AD,OE∥AD,
∴OE⊥CD,
又∵OF=FE,
∴四边形OCED是菱形.
点评 本题考查了矩形的性质以及菱形的判定,理解菱形的判定方法是关键.

练习册系列答案
相关题目
3.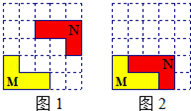 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
 在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )
在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是( )| A. | 先向下移动1格,再向左移动1格 | B. | 先向下移动1格,再向左移动2格 | ||
| C. | 先向下移动2格,再向左移动1格 | D. | 先向下移动2格,再向左移动2格 |
7.在四边形ABCD中,AD∥BC,∠B=∠C,要使四边形ABCD为矩形,还需添加一个条件,这个条件可以是( )
| A. | AB=CD | B. | AC=BD | C. | ∠A=∠D | D. | ∠A=∠B |
4.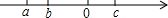 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
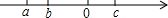 实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )
实数a,b,c在数轴上的位置如图所示,则化简$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{{c}^{2}}$-$\sqrt{{(a-c)}^{2}}$-$\sqrt{{(b+c)}^{2}}$的结果为( )| A. | a-2b | B. | 2b+c | C. | -2a+c | D. | a-2b+c |
1. 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
 如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )
如图,在?ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE、EC的长度分别为( )| A. | 1和4 | B. | 4和1 | C. | 2和3 | D. | 3和2 |
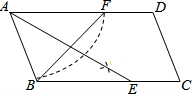 如图,?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为8.
如图,?ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E,若BF=6,AB=5,则AE的长为8.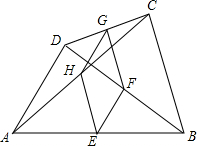 如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.
如图,在四边形ABCD中,E、F、G、H分别是AB、CD、AC、BD的中点.