题目内容
12.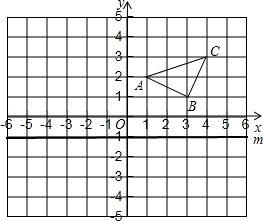 如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).
如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).(1)直接写出点C关于y轴的对称点的坐标;
(2)作△ABC关于直线m(直线m上各点的纵坐标都为-1)的对称图形△A1B1C1,写出点C关于直线m的对称点C1的坐标;
(3)点P是坐标轴上一点,使△ABP是等腰三角形,则符合条件的点P的个数有6.
分析 (1)直接利用关于y轴对称点的性质得出答案;
(2)直接利用轴对称的性质得出对应点位置进而得出答案;
(3)利用等腰三角形的性质得出符合题意答案.
解答  解:(1)点C关于y轴的对称点的坐标为:(-4,3);
解:(1)点C关于y轴的对称点的坐标为:(-4,3);
(2)如图所示:△A1B1C1,即为所求,点C关于直线m的对称点C1的坐标为:(4,-5);
(3)如图所示:△ABP是等腰三角形,P1,P2,P3,P4都符合题意,以及AB的垂直平分线会与坐标轴有两个交点,故符合条件的点P的个数有6.
点评 此题主要考查了轴对称变换以及等腰三角形的判定,正确得出对应点位置是解题关键.

练习册系列答案
相关题目
2.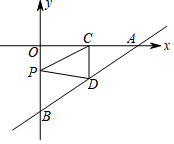 如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
 如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )
如图,直线y=$\frac{2}{3}$x-4分别与x轴、y轴交于点A和点B,点C、D分别是线段OA、AB的中点,点P为OB上一动点,当PC+PD取最小值时点P的坐标是( )| A. | (0,-1) | B. | (0,-2) | C. | (0,-3) | D. | (0,-4) |
 概念理解:
概念理解: 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).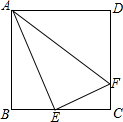 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,且CD=4CF.求证:∠AEF=90°.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,且CD=4CF.求证:∠AEF=90°. 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合,折痕EF,若长方形的长BC为8,宽AB为4,则△AEF的面积为10.
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合,折痕EF,若长方形的长BC为8,宽AB为4,则△AEF的面积为10. 如图,∠1=47°,∠2=133°,∠D=47°,那么图中哪些线段平行?并说明理由.
如图,∠1=47°,∠2=133°,∠D=47°,那么图中哪些线段平行?并说明理由. 如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC于D,AB=15,BD=9,CD=5,则⊙O的半径为$\frac{65}{8}$.
如图,△ABC内接于⊙O,AE是⊙O的直径,AD⊥BC于D,AB=15,BD=9,CD=5,则⊙O的半径为$\frac{65}{8}$.