题目内容
7. 如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合,折痕EF,若长方形的长BC为8,宽AB为4,则△AEF的面积为10.
如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合,折痕EF,若长方形的长BC为8,宽AB为4,则△AEF的面积为10.
分析 设FC=x,则BF=8-x,在Rt△ABF中利用勾股定理求出x的值,进而可得出△AEF的面积.
解答 解:设FC=x,则BF=8-x,
∵四边形ABCD为长方形,
∴△ABF为Rt△,
∴AB2+BF2=AF2,即42+(8-x)2=x2,解得x=5,
∵AD∥BC,
∴∠AEF=∠EFC,
由图形反折变换的性质可知,∠AFE=∠EFC,AD′=CD=AB,
∴∠AEF=∠AFE,
∴AE=AF=CF=5,
∴△AEF的面积=$\frac{1}{2}×$5×4=10,
故答案为:10.
点评 本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.

练习册系列答案
相关题目
15.正方形的面积是5,它的对角线长是( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{10}$ |
16.下列说法中错误的是( )
| A. | 368万精确到个位 | B. | 2.58精确到百分位 | ||
| C. | 5.7×102精确到十位 | D. | 566精确到个位 |
17.小米家位于公园的正东100米处,从小米家出发向北走250米就到小华家,若选取小华家为原点,分别以正东,正北方向为x轴,y轴正方向建议平面直角坐标系,则公园的坐标是( )
| A. | (-250,-100) | B. | (100,250) | C. | (-100,-250) | D. | (250,100) |
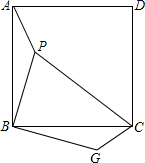 如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.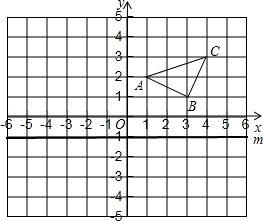 如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).
如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3). 如图,Rt△ABC中,∠ACB=90°,AC=6,BC=5,则以AB为边长的正方形的面积是61.
如图,Rt△ABC中,∠ACB=90°,AC=6,BC=5,则以AB为边长的正方形的面积是61.