题目内容
20.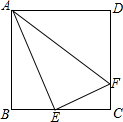 如图,正方形ABCD中,E是BC的中点,F是CD上的一点,且CD=4CF.求证:∠AEF=90°.
如图,正方形ABCD中,E是BC的中点,F是CD上的一点,且CD=4CF.求证:∠AEF=90°.
分析 利用正方形的性质得出AB=BC=CD=DA,∠B=∠C=∠D=90°,设出边长为a,进一步利用勾股定理求得AE、EF、AF的长,再利用勾股定理逆定理判定即可.
解答 证明:∵四边形ABCD为正方形,
∴AB=BC=CD=DA,∠B=∠C=∠D=90°.
设AB=BC=CD=DA=a,
∵E是BC的中点,且4CF=CD,
∴BE=EC=$\frac{1}{2}$a,CF=$\frac{1}{4}$a,
在Rt△ABE中,由勾股定理可得AE2=AB2+BE2=$\frac{5}{4}$a2,
同理可得:EF2=EC2+FC2=$\frac{5}{16}$a2,AF2=AD2+DF2=$\frac{25}{16}$a2,
∵AE2+EF2=AF2,
∴△AEF为直角三角形,
∴∠AEF=90°.
点评 此题考查正方形的性质,勾股定理、勾股定理逆定理的运用,注意在正方形中的直角三角形的应用.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
10.已知点P(2-a,a)在平面直角坐标系的第四象限内,则直线y=ax+3不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
15.正方形的面积是5,它的对角线长是( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{10}$ |
9. 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
 如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )
如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=$\frac{1}{4}$CD,下列结论:①∠BAE=30°;②△ABE∽△AEF;③△ABE∽△ECF;④△ADF∽△ECF.其中正确的是( )| A. | ①②③ | B. | ②③ | C. | ③④ | D. | ②③④ |
10.下列调查中,最适合采用抽样调查的是( )
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 选出某校短跑最快的学生参加全市比赛 | |
| D. | 了解某批次灯泡的使用寿命情况 |
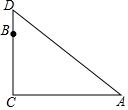 在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.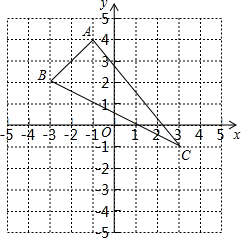 如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).
如图,已知△ABC的三个顶点分别为A(-1,4)、B(-3,2)、C(3,-1).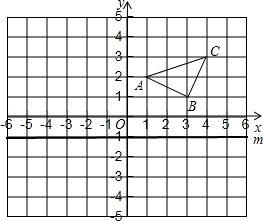 如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).
如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).