题目内容
2. 概念理解:
概念理解:把多边形的某些边向两端延长,其他各边若不全在延长所得直线的同侧,则把这样的多边形叫做凹多边形.如图,四边形ABCD中,延长BC,边AB、CD分别在直线BC的两侧,所以四边形ABCD是一个凹四这形.
探索性质:
(1)请结合右图证明凹四边形的内角和为360°;
已知:四边形ABCD为凹四边形.
求证:四边形ABCD内角和为360°.
证明:
(2)请写出两个关于凹六边形的正确结论.
①凹六边形外角和360°;
②凹六边形内角和720°.
分析 (1)题设部分作为已知条件,结论部分作为求证即可解决问题;
(2)①凹六边形外角和360°.②凹六边形内角和720°;
解答 解:(1)已知:四边形ABCD为凹四边形.
求证:四边形ABCD内角和为360°.
证明:如图,延长BC与AD交于E.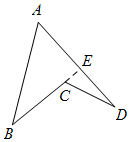
四边形内角和=∠A+∠B+∠BCE+∠ECD+∠D,
∵B、C、E共线.
∴∠AEB为△CDE的一个外角.
∴∠D+∠ECD=∠AEB,
又∠A、∠B、∠AEB△AEB的三个内角.
∴∠A+∠B+∠AEB=180°,
∵∠BCE=180°,
∴四边形内角和为180°=180°=360°,
(2)①凹六边形外角和360°.
②凹六边形内角和720°.
故答案分别为:四边形ABCD为凹四边形,四边形ABCD内角和为360°,凹六边形外角和360°,凹六边形内角和720°.
点评 本题考查多边形的内角与外角的性质,解题的关键是理解题意没学会添加常用辅助线解决问题,属于中考基础题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
10.已知点P(2-a,a)在平面直角坐标系的第四象限内,则直线y=ax+3不经过第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
7.等腰三角形的两边长分别为2cm和5cm,则这个三角形的周长为( )
| A. | 12cm | B. | 9cm | C. | 7cm | D. | 12cm或9cm |
14.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a2•a5=a7 | C. | (2a)3=2a3 | D. | 3a8÷a2=3a4 |
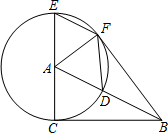 如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.
如图,已知⊙A的半径为4,EC是圆的直径,点B是⊙A的切线CB上的一个动点,连接AB交⊙A于点D,弦EF平行于AB,连接DF,AF.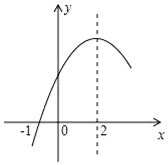 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.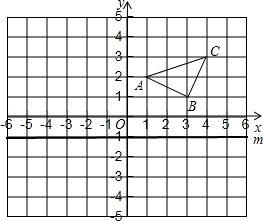 如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).
如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).