题目内容
3.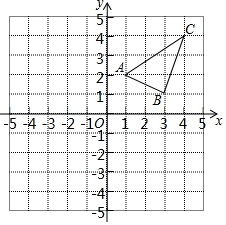 学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).
学习完轴对称后,黑板展示区出了一道作图题(不写作法,保留作图痕迹).①画出△ABC关于y轴对称的△A1B1C1,并直接写出△A1B1C1三个顶点的坐标.
②在x轴上求作一点P,使PA1+PC最小.
③计算出△A1AP的面积.
分析 ①直接利用关于y轴对称点的性质得出对应点位置进而得出答案;
②直接利用轴对称得出A1关于x轴对应点A′的位置,进而连接A′C,即可得出P点位置;
③直接利用三角形面积求法得出答案.
解答  解:①如图所示:△A1B1C1,即为所求,A1(-1,2),B1(-3,1),C1(-4,4);
解:①如图所示:△A1B1C1,即为所求,A1(-1,2),B1(-3,1),C1(-4,4);
②如图所示:点P即为所求,此时PA1+PC最小;
③△A1AP的面积为:$\frac{1}{2}$×AA1×2=2.
点评 此题主要考查了轴对称变换以及轴对称求最短路线,正确得出对应点位置是解题关键.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
14.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a2•a5=a7 | C. | (2a)3=2a3 | D. | 3a8÷a2=3a4 |
15.正方形的面积是5,它的对角线长是( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{10}$ |
13.一次函数y=kx+b(k≠0)的图象经过点B(2,0),C(0,6)两点,则kx+b≥2x的解集是( )
| A. | x≤$\frac{6}{5}$ | B. | x<2 | C. | x$<\frac{6}{5}$ | D. | x≤2 |
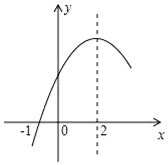 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a-3b+c>0;(3)4a+2b>m(am+b),(m≠2的实数)(4)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论有( )个.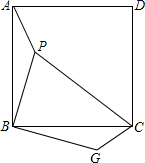 如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.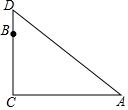 在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.
在一棵树的10米高处有两个猴子为抢吃池塘边水果,一只猴子爬下树跑到A处(离树20米)的池塘边.另一只爬到树顶D后直接跃到A处,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高15米.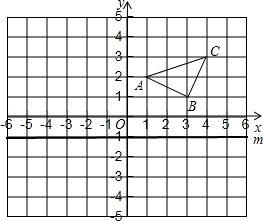 如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).
如图,在平面直角坐标系中,已知A(1,2)、B(3,1)、C(4,3).