题目内容
14.观察以下等式:$\frac{1}{1×2}=1-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$…(1)通过观察,在横线上填入正确答案 $\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;(其中n为正整数)
(2)设$a=\frac{1}{1×3}+\frac{1}{3×5}+\frac{1}{5×7}+…+\frac{1}{(2n-1)(2n+1)}$,$b=\frac{1}{2}$,类比(1)的思想,你能比较出a、b的大小吗?证明你的结论.
分析 (1)观察所给算式,找出其中的规律,然后依据规律可得出答案;
(2)先求得a的值,然后再比较大小即可.
解答 解:(1)$\frac{1}{n(n+1)}$=$\frac{1}{n}-\frac{1}{n+1}$;
故答案为:$\frac{1}{n}-\frac{1}{n+1}$.
(2)a=$\frac{1}{2}(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}+\frac{1}{2n+1})$=$\frac{1}{2}$(1$-\frac{1}{2n+1}$)=$\frac{1}{2}•\frac{2n}{2n+1}$=$\frac{n}{2n+1}$$<\frac{1}{2}$.
∴a<b.
点评 本题主要考查的是求代数式的值,拆项裂项法的应用是解题的关键.

练习册系列答案
相关题目
6.若一次函数y=2x-4上有一点的坐标是(3,2),则方程2x-y-4=0必有一个解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$.
4.下列各式中,正确的是( )
| A. | -(-1)<-(+2) | B. | -$\frac{5}{6}>-\frac{5}{7}$ | C. | -(-5$\frac{1}{2}$)>|-5.5| | D. | -$\frac{7}{8}$$<-\frac{6}{7}$ |
 在△ABC中,AB=10,∠C=100°,求△ABC外接圆⊙O的半径r.(用三角函数表示)
在△ABC中,AB=10,∠C=100°,求△ABC外接圆⊙O的半径r.(用三角函数表示)
 如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?
如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?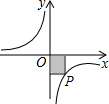 如图,P是反比例函数的图象上的一点,过点P分别向x轴、y轴作垂线,所得到的图中的阴影部分的面积为6,则该反比例函数的表达式为y=-$\frac{6}{x}$.
如图,P是反比例函数的图象上的一点,过点P分别向x轴、y轴作垂线,所得到的图中的阴影部分的面积为6,则该反比例函数的表达式为y=-$\frac{6}{x}$.