题目内容
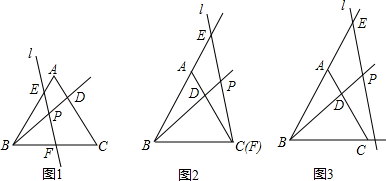
已知△ABC与△ADE均为等边三角形,点A,E在BC的同侧.
(1)如图甲,点D在BC上,求证:CE+CD=AC;
(2)如图乙,若点D在BC的延长线上,其它条件不变,上述结论是否成立?若成立,请予以证明,若不成立,请说明理由.

(1)如图甲,点D在BC上,求证:CE+CD=AC;
(2)如图乙,若点D在BC的延长线上,其它条件不变,上述结论是否成立?若成立,请予以证明,若不成立,请说明理由.

考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)先证明△ABD≌△ACE,得出BD=CE,即可证出CE+CD=BD+CD=BC=AC;
(2)先证明△ABD≌△ACE,得出BD=CE,即可证出CE-CD=BD-CD=BC=AC.
(2)先证明△ABD≌△ACE,得出BD=CE,即可证出CE-CD=BD-CD=BC=AC.
解答:解:(1)证明:∵△ABC和△ADE均为等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE+CD=BD+CD=BC=AC;
(2)上述结论不成立,CE-CD=AC;
∵△ABC和△ADE均为等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE-CD=BD-CD=BC=AC.
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE+CD=BD+CD=BC=AC;
(2)上述结论不成立,CE-CD=AC;
∵△ABC和△ADE均为等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
|
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE-CD=BD-CD=BC=AC.
点评:本题考查了等边三角形的性质和全等三角形的判定与性质;证明三角形全等是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
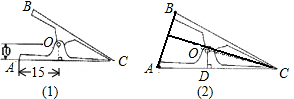 夹文件或试卷用的铁夹子在常态下的侧面示意图如图所示,它是轴对称图形,AC,BC表示铁夹子的两个面,点O是轴,OD⊥AC于点D,已知OD=10mm,OC=26mm,AD=15mm.
夹文件或试卷用的铁夹子在常态下的侧面示意图如图所示,它是轴对称图形,AC,BC表示铁夹子的两个面,点O是轴,OD⊥AC于点D,已知OD=10mm,OC=26mm,AD=15mm.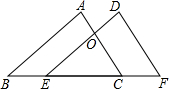 已知,如图,点B、E、C、F四点在同一条直线上,AB∥DE,AB=DE,AC、DE相交于点O,BE=CF.求证:AC=DF.
已知,如图,点B、E、C、F四点在同一条直线上,AB∥DE,AB=DE,AC、DE相交于点O,BE=CF.求证:AC=DF.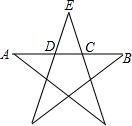 如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.
如图,在五角星图形中,AD=BC,C,D两点都是AB的黄金分割点,AB=1,求CD的长.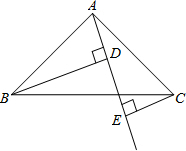 如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.
如图,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的两侧,BD⊥AE于点D,CE⊥AE于点E. 如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E,BD,CE相交于点F,BE与CD相等吗?请说明理由.
如图,AB=AC,BD⊥AC,CE⊥AB,垂足分别为D,E,BD,CE相交于点F,BE与CD相等吗?请说明理由.