题目内容
1.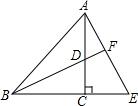 如图,在△ABC中,∠ACB=90°,D为AC上一点,延长BC到点E,使CE=CD,连接AE且与BD的延长线交于点F,若AE=BD,求证:BD⊥AE.
如图,在△ABC中,∠ACB=90°,D为AC上一点,延长BC到点E,使CE=CD,连接AE且与BD的延长线交于点F,若AE=BD,求证:BD⊥AE.
分析 根据HL证明Rt△BDC与Rt△AEC全等,再利用对应角的关系解答即可.
解答 证明:∵在△ABC中,∠ACB=90°,
∴∠DCB=∠ACE=90°,
在Rt△BDC与Rt△AEC中,
$\left\{\begin{array}{l}{AE=BD}\\{DC=CE}\end{array}\right.$,
∴Rt△BDC≌Rt△AEC(HL),
∴∠DBC=∠CAE,
∵∠DBC+∠BDC=90°,∠BDC=∠ADF,
∴∠ADF+∠DAF=90°,
∴BD⊥AE.
点评 此题考查全等三角形的判定和性质,关键是根据HL证明Rt△BDC与Rt△AEC全等.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
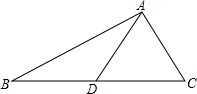 如图,AD是△ABC的中线.
如图,AD是△ABC的中线.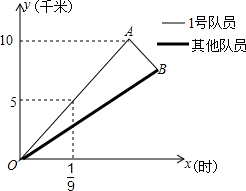 自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.
自行车队点的一次训练中,1号队员以高于其他队员10千米/时的速度独自前行,匀速行进一段时间后,又返回队伍,在往返过程中速度保持不变,设分开后行进的时间为x小时,1号队员和其他队员行进的路程分别为y1、y2(千米),且y1、y2与x的函数关系如图所示.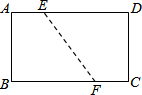 如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,则折痕EF的长为7.5.
如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠,使B点与D点重合,则折痕EF的长为7.5.