题目内容
 如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=| m |
| x |
(1)k=
(2)求反比例函数的解析式;
(3)根据图象直接写出关于x的不等式,0<kx-1<
| m |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据三角形面积求出OA,得出A、B的坐标,代入一次函数的解析式即可求出解析式,把x=8代入求出D的坐标,把D的坐标代入反比例函数的解析式求出即可;
(2)求出两函数的另一个交点,即可得出答案.
(3)根据函数图象可得答案.
(2)求出两函数的另一个交点,即可得出答案.
(3)根据函数图象可得答案.
解答:
解:(1)∴OB=2,
∴B(-2,0),
代入y=kx-1得:0=-2k-1,
解得:k=-
,
故答案为-
;
(2)∵k=-
,
∴一次函数y=-
x-1,
∵OB=BD=2,
∴OD=4,
∴C的横坐标为-4,
代入y=-
x-1得y=1,
∴C(-4,1),
∴反比例函数的解析式是y=-
;
(3)根据图象可知关于x的不等式,0<kx-1<
的解集为-4<x<-2.
∴B(-2,0),
代入y=kx-1得:0=-2k-1,
解得:k=-
| 1 |
| 2 |
故答案为-
| 1 |
| 2 |
(2)∵k=-
| 1 |
| 2 |
∴一次函数y=-
| 1 |
| 2 |
∵OB=BD=2,
∴OD=4,
∴C的横坐标为-4,
代入y=-
| 1 |
| 2 |
∴C(-4,1),
∴反比例函数的解析式是y=-
| 4 |
| x |
(3)根据图象可知关于x的不等式,0<kx-1<
| m |
| x |
点评:本题考查了用待定系数法求出函数的解析式,一次函数和和反比例函数的交点问题,函数的图象的应用,主要考查学生的观察图形的能力和计算能力.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
下列结论错误的是( )
| A、sin60°-sin30°=sin30° | ||
| B、sin30°=cos60° | ||
C、tan60°=
| ||
| D、sin245°+cos245°=1 |
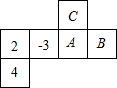 如图是一个正方体的展开图,若正方体相对的面上的两个数互为相反数,则A,B,C三个数依次是( )
如图是一个正方体的展开图,若正方体相对的面上的两个数互为相反数,则A,B,C三个数依次是( )| A、-2,-4,3 |
| B、3,-2,-4 |
| C、-2,3,-4 |
| D、3,-4,-2 |
三角形中,到三个顶点距离相等的点是( )
| A、三条高线的交点 |
| B、三条中线的交点 |
| C、三条角平分线的交点 |
| D、三边垂直平分线的交点 |
 如图,矩形ABCD中,AB=1,AD=a,以点A为圆心,a为半径画弧,交BC于点E,交AB延长线于点F,当两个阴影部分面积相等时,a的值是
如图,矩形ABCD中,AB=1,AD=a,以点A为圆心,a为半径画弧,交BC于点E,交AB延长线于点F,当两个阴影部分面积相等时,a的值是 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.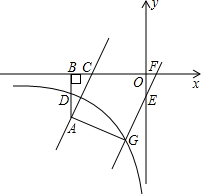 如图,点A在反比例函数y=
如图,点A在反比例函数y= 如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.
如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.