题目内容
 如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.
如图,点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=10,试求△PMN的周长.考点:轴对称的性质
专题:
分析:根据轴对称的性质可得PM=P1M,PN=P2N,再求出△PMN的周长=P1P2,从而得解.
解答:
解:∵P点关于OA、OB的对称点P1,P2,
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN,
=P1M+MN+P2N,
=P1P2,
∵P1P2=10,
∴△PMN的周长=10.
∴PM=P1M,PN=P2N,
∴△PMN的周长=PM+MN+PN,
=P1M+MN+P2N,
=P1P2,
∵P1P2=10,
∴△PMN的周长=10.
点评:本题考查了轴对称的性质,熟记对称轴上的任何一点到两个对应点之间的距离相等是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2014年金华市实现生产总值(GDP)3206亿元,按可比价计算,比上年增长8.3%.用科学记数法表示2014年金华市的生产总值为( )
| A、32.06×1012元 |
| B、3.206×1011元 |
| C、3.206×1010元 |
| D、3.206×1012元 |
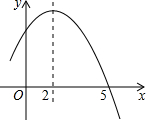 如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )
如图是二次函数y=ax2+bx+c的部分图象,由图象可知不等式ax2+bx+c>0的解集是( )| A、-1<x<5 |
| B、x>5 |
| C、x<-1且x>5 |
| D、x<-1或x>5 |
 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.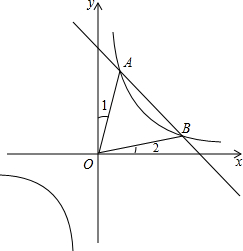 如图已知函数y1=
如图已知函数y1= 如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=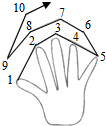 请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢?
请同学们伸出左手,一起做下面的游戏:从大拇指开始,依次数数字1、2、3、4、5,然后从无名指开始倒着数6、7、8、9,再从食指开始数10、11、12、13,…请问数字20落在哪个手指上?200?2000呢? (1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
(1)已知⊙O的直径为10cm,点A为⊙O外一定点,OA=12cm,点P为⊙O上一动点,求PA的最大值和最小值.
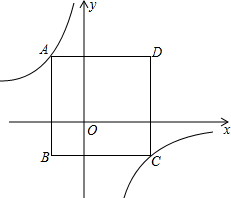 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=