题目内容
 如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.
如图,在梯形ABCD中,AB∥CD,AD=DC=BD=a,BC=b,求AC的长.考点:梯形,勾股定理,圆周角定理
专题:
分析:首先得出A,B,C在以点D为圆心DC长为半径的圆上,延长AD交圆D于点E,连接AC,EC,进而利用等腰三角形的性质以及平行线的性质求出∠BDC=∠CDE,即可得出△CDB≌△CDE(SAS),再利用勾股定理得出AC的长.
解答: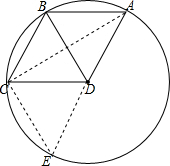 解:由题意可得:A,B,C在以点D为圆心DC长为半径的圆上,延长AD交圆D于点E,
解:由题意可得:A,B,C在以点D为圆心DC长为半径的圆上,延长AD交圆D于点E,
连接AC,EC,
∵AB∥CD,
∴∠ABD=∠BDC,∠BAD=∠CDE,
∵BD=AD,
∴∠DBA=∠DAB,
∴∠BDC=∠CDE,
在△CDB和△CDE中
,
∴△CDB≌△CDE(SAS),
∴BC=EC=b,
∵AE=AD+DE=2a,
故在Rt△ACE中.
AC=
=
.
 解:由题意可得:A,B,C在以点D为圆心DC长为半径的圆上,延长AD交圆D于点E,
解:由题意可得:A,B,C在以点D为圆心DC长为半径的圆上,延长AD交圆D于点E,连接AC,EC,
∵AB∥CD,
∴∠ABD=∠BDC,∠BAD=∠CDE,
∵BD=AD,
∴∠DBA=∠DAB,
∴∠BDC=∠CDE,
在△CDB和△CDE中
|
∴△CDB≌△CDE(SAS),
∴BC=EC=b,
∵AE=AD+DE=2a,
故在Rt△ACE中.
AC=
| AE2-EC2 |
| 4a2-b2 |
点评:此题主要考查了勾股定理的应用、等腰三角形的性质、全等三角形的判定与性质等知识,作辅助线构造出全等三角形和直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| 17 |
| A、2到3之间 |
| B、3到4之间 |
| C、4到5之间 |
| D、5到6之间 |
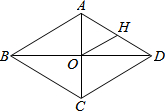 如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形ABCD的周长为36,则OH的长等于( )
如图所示,菱形ABCD中,对角线AC、BD相交于点O,H为AD边的中点,菱形ABCD的周长为36,则OH的长等于( )| A、4.5 | B、5 | C、6 | D、9 |
-
与
在数轴上对应点的位置如图所示,则数轴上被圈住的表示整数的点的个数为( 
| 2 |
| 10 |

| A、2个 | B、3个 | C、4个 | D、5个 |
等腰三角形一腰上的高与腰长之比为1:2,则等腰三角形顶角的度数为( )
| A、60° |
| B、120° |
| C、30°或150° |
| D、60°或120° |
 如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
如图,一次函数y=kx-1的图象与坐标轴分别交于A、B两点,与反比例函数y=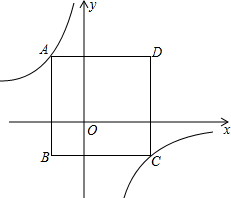 如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=
如图,边长为6的正方形ABCD置于平面直角坐标系xOy中,且AB平行于y轴,已知点A的横坐标为-2,反比例函数y=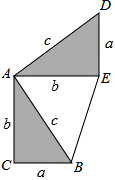 勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.
勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中常见的是“面积法”,当两个全等的直角三角形如图摆放时(其中∠DAB=90°),就可以用“面积法”来证明勾股定理,即证明a2+b2=c2,请你写出勾股定理的证明过程.