题目内容
18.化简:(1)先化简,再求值:x(x2+1)-x2(x-3)-3(x2+x)-2,其中x=-$\frac{1}{2}$.
(2)先化简,再求值:$\frac{a}{a+2}$-$\frac{1}{a+1}$÷$\frac{a+2}{{a}^{2}+2a+1}$,其中a=3$\sqrt{2}$-2.
分析 (1)去括号,合并同类项;再代入求值;
(2)先将分式的分子分母因式分解,同时将除法转化为乘法,再计算分式的乘法,最后计算分式的减法即可.
解答 解:(1)x(x2+1)-x2(x-3)-3(x2+x)-2,
=x3+x-x3+3x2-3x2-3x-2,
=-2x-2,
当x=-$\frac{1}{2}$时,原式=-2×$(-\frac{1}{2})$-2=-1;
(2)$\frac{a}{a+2}$-$\frac{1}{a+1}$÷$\frac{a+2}{{a}^{2}+2a+1}$,
=$\frac{a}{a+2}$-$\frac{1}{a+1}$$•\frac{(a+1)^{2}}{a+2}$,
=$\frac{a}{a+2}$-$\frac{a+1}{a+2}$,
=$\frac{a-a-1}{a+2}$,
=-$\frac{1}{a+2}$,
当a=3$\sqrt{2}$-2时,原式=-$\frac{1}{3\sqrt{2}-2+2}$,
=-$\frac{1}{3\sqrt{2}}$,
=-$\frac{\sqrt{2}}{6}$.
点评 本题主要考查整式的化简求值及分式的混合运算,熟练掌握分式和整式的混合运算顺序和运算法则是解题的关键.

练习册系列答案
相关题目
8.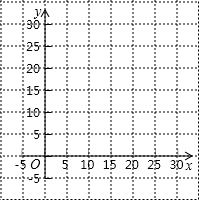 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
(1)根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图象,猜测y与x之间的函数关系,并求出该函数关系式:
(2)设经营此笔记本的日销售利润为w元,试求出w与x之间的函数关系式;
(3)当日销售单价为8元时,求日销售利润是多少元?
 某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:
某商场出售一批进价为每个2元的笔记本,在市场营销中发现此商品的日销售单价x(元)与日销售量y(个)之间有如下关系:(1)根据表中数据在平面直角坐标系中描出实数x,y的对应点,用平滑曲线连接这些点,并观察所得的图象,猜测y与x之间的函数关系,并求出该函数关系式:
| x(元) | 3 | 4 | 5 | 6 |
| y(个) | 20 | 15 | 12 | 10 |
(3)当日销售单价为8元时,求日销售利润是多少元?
13. 如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )
如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )
 如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )
如图所示,△ACE≌△DBF,AE∥DF,AD=6,BC=2,则AB的长度等于( )| A. | 2 | B. | 8 | C. | 6 | D. | 3 |
10.如果xm=4,xn=8(m、n为自然数),那么x3m-n等于( )
| A. | $\frac{3}{2}$ | B. | 4 | C. | 8 | D. | 56 |
 某小区有一块长20米,宽15米的长方形空地,在上面修建了如图所示的十字形步道,步道均为长方形,宽度均为x米,在步道以外的其余部分种上了花草.
某小区有一块长20米,宽15米的长方形空地,在上面修建了如图所示的十字形步道,步道均为长方形,宽度均为x米,在步道以外的其余部分种上了花草.
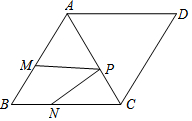 已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$.
已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$. 如图,已知∠AOC=∠BOD=90°,∠AOD=130°,则∠BOC=50°.
如图,已知∠AOC=∠BOD=90°,∠AOD=130°,则∠BOC=50°.