题目内容
7.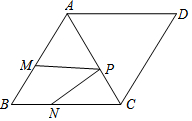 已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$.
已知菱形ABCD中,∠B=60°,AD=4$\sqrt{2}$,点P、M、N分别为AC、AB、BC上的动点,则PM+PN的最小值是2$\sqrt{6}$.
分析 如图,作AH⊥BC于H.首先证明△ABC,△ADC的是等边三角形,作点M关于直线AC的对称点M′,因为PM+PN=PM′+PN,所以欲求PM+PN是最小值,只要求PM′+PN的最小值,所以根据垂线段最短,当M″、P、N′共线时,M″N′⊥BC时,PM″+PN′的值最小,易证四边形AHN′M″是矩形,所以N′M″=AH=AB•sin60°,由此即可解决问题.
解答 解:如图,作AH⊥BC于H.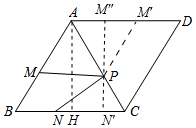
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,
∵∠B=∠D=60°,
∴△ABC,△ADC的是等边三角形,
作点M关于直线AC的对称点M′,
∵PM+PN=PM′+PN,
∴欲求PM+PN是最小值,只要求PM′+PN的最小值,
∴根据垂线段最短,
当M″、P、N′共线时,M″N′⊥BC时,PM″+PN′的值最小,
易证四边形AHN′M″是矩形,
∴N′M″=AH=AB•sin60°=4$\sqrt{2}$•$\frac{\sqrt{3}}{2}$=2$\sqrt{6}$,
故答案为2$\sqrt{6}$.
点评 本题考查轴对称最短问题、菱形的性质、等边三角形的判定和性质、垂线段最短等知识,解题的关键是学会用转化的思想思考问题,把最短问题转化为垂线段最短,属于中考常考题型.

练习册系列答案
相关题目
17.若单项式2x2ya+b与3xa-by4是同类项,则a,b的值分别是( )
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
15.下列计算中,不正确的是( )
| A. | a2•a5=a10 | B. | a2-2ab+b2=(a-b)2 | C. | -(a-b)=b-a | D. | 3a3b2÷a2b2=3a |
2.某餐厅共有10名员工,所有员工的工资情况如下表:
则该餐厅所有员工工资的众数、中位数分别是( )
| 人员 | 经理 | 厨师 | 会计 | 保安 | 服务员 |
| 人数(人) | 1 | 2 | 1 | 1 | 5 |
| 工资(元) | 5000 | 4000 | 3500 | 3000 | 2000 |
| A. | 5000,3500 | B. | 5000,2500 | C. | 2000,3500 | D. | 2000,2500 |
16.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{x-1}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{1}{16}}$ | D. | $\sqrt{9{a^2}}$ |
 如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,求该图形的面积.
如图,AD=8,CD=6,∠ADC=90°,AB=26,BC=24,求该图形的面积. 如图,
如图,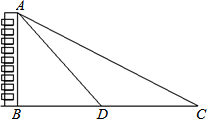 如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.
如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.