题目内容
9.若关于x的不等式mx-n>0的解集是x<$\frac{1}{4}$,则关于x的不等式(m-n)x>m+n的解集是x<$\frac{5}{3}$.分析 根据已知求出m<0和m=4n,求出m-n<0,根据不等式的性质得出即可.
解答 解:∵mx-n>0,
∴mx>n,
∵mx-n>0的解集是x<$\frac{1}{4}$,
∴m<0,$\frac{n}{m}$=$\frac{1}{4}$,
∴m=4n,
∴n<0,m-n=3n<0,m+n=5n,
∴关于x的不等式(m-n)x>m+n的解集为x<$\frac{m+n}{m-n}$,即x<$\frac{5}{3}$,
故答案为:x<$\frac{5}{3}$.
点评 本题考查了解一元一次不等式,能求出m-n=3n<0和m<0是解此题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
17.若单项式2x2ya+b与3xa-by4是同类项,则a,b的值分别是( )
| A. | a=3,b=1 | B. | a=-3,b=1 | C. | a=3,b=-1 | D. | a=-3,b=-1 |
14.若|a|=3,b=1,则ab=( )
| A. | 3 | B. | -3 | C. | 3或-3 | D. | 无法确定 |
1.在“书香伍家”读书节活动中,21名志愿者参与整理一批图书,每人每小时能登记录入20本或摆放120本书籍,为使每小时登记录入的书籍正好被及时摆放,设x名志愿者参与登记录入,其余志愿者参与摆放,则所列方程正确的是( )
| A. | 20x=120(21+x) | B. | 120x=20(21-x) | C. | 20x=120(21-x) | D. | 120x=20(21+x) |
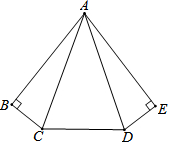 已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.
已知五边形ABCDE中,∠B=∠E=90°,AB=AE,AC=AD,∠BCD=140°.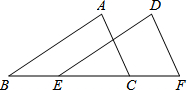 如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.
如图,△ABC≌△DEF,∠A和∠D是对应角,AB和DE是对应边,那么还有对应角是∠B=∠E,∠C=∠F,对应边是BC=EF,AC=DF.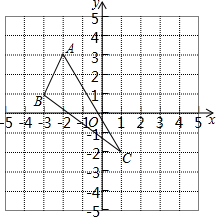 如图,
如图,