题目内容
12.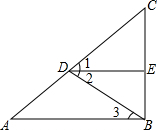 在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,
在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,求证:∠A=∠3.
证明:∵DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直定义)
∴DE∥AB(同位角相等,两直线平行)
∴∠2=∠3 (两直线平行,内错角相等)
∠1=∠A (两直线平行,同位角相等)
又∠1=∠2(已知),
∴∠A=∠3(等量代换)
分析 根据垂直的定义得到∠DEC=∠ABC=90°,根据同位角相等两直线平行得到DE∥AB,根据平行线的性质得到∠2=∠3,∠1=∠A,等量代换即可得到结论.
解答 证明:∵DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直定义)
∴DE∥AB(同位角相等,两直线平行)
∴∠2=∠3(两直线平行,内错角相等)
∠1=∠A(两直线平行,同位角相等)
又∠1=∠2(已知),
∴∠A=∠3(等量代换),
故答案为:垂直定义,∠3,同位角相等,两直线平行,∠A,两直线平行,同位角相等.
点评 此题主要考查了平行的判定和性质,关键是掌握内错角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3. 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
 把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )
把一张对边互相平行的纸条折成如图所示的样子,EF是折痕,如果∠EFB=32°,那么下列结论:①∠CEF=32°;②∠AEF=148°;③∠BGE=64°;④∠BFD=116°正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
7.函数y=$\frac{x-2}{x+1}$+x中x的取值范围为( )
| A. | x≠1 | B. | x≠-1 | C. | x≠-2 | D. | x≠2 |
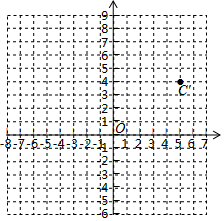 在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3).
在平面直角坐标系中,A,B,C三点的坐标分别为(-6,7)、(-3,0)、(0,3). 已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.
已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M. 如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$).
如图,平面直角坐标系中,已知直线y=x上一点P(1,1),C为y轴上一点,连接PC,线段PC绕点P顺时针旋转90°至线段PD,过点D作直线AB⊥x轴,垂足为B,直线AB与直线y=x交于点A,且BD=3AD,连接CD,直线CD与直线y=x交于点Q,则点Q的坐标为($\frac{32}{15}$,$\frac{32}{15}$). 如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米?
如图,AB是电线杆,从距离地面12m高的A处,向离电杆5m的B处埋线,并埋入地下1.5m深,求拉线长多少米? 如图,A,B在一水池的两侧,若BE=DE,∠B=∠D=90°,点A,E,C在同一条直线上,CD=8cm,则水池宽AB=8m.
如图,A,B在一水池的两侧,若BE=DE,∠B=∠D=90°,点A,E,C在同一条直线上,CD=8cm,则水池宽AB=8m.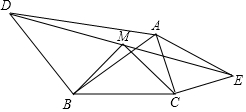 己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.
己知:如图,若△ABD和△ACE为等腰Rt△,AB=DB,AC=CE,M为DE中点,求证:△BMC为等腰Rt△.