题目内容
20. 已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.
已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.(1)求该抛物线的表达式;
(2)如果点P的横坐标为2,点Q是第一象限抛物线上的一点,且△QMC和△PMC的面积相等,求点Q的坐标;
(3)如果PM=$\frac{3}{2}$PN,求tan∠CMN的值.
分析 (1)根据点B、C的坐标利用待定系数法,即可求出抛物线的表达式;
(2)根据点B、C的坐标利用待定系数法,求出直线BC的表达式,由点P的横坐标,即可求出点P、M的坐标,进而可求出△PMC的面积,根据△QMC和△PMC的面积相等,可求出点Q的纵坐标为1,再利用二次函数图象上点的坐标特征结合点Q在第一象限,即可求出点Q的坐标,此题得解;
(3)过点C作CH⊥MN,垂足为H,设M(m,-m2+2m+3)(0<m<3),则P(m,-m+3),由PM=$\frac{3}{2}$PN,可求出m的值,从而得出点M、P的坐标,进而可求出MH、CH的值,再根据正切的定义,即可求出tan∠CMN的值.
解答 解:(1)将B(3,0)、C(0,3)代入y=-x2+bx+c,
得:$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$.
∴抛物线的表达式为y=-x2+2x+3.
(2)依照题意画出图形,如图1所示.
设直线BC的表达式为y=kx+b(k≠0),
将点C(0,3)、B(3,0)代入y=kx+b,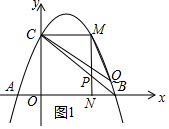
得:$\left\{\begin{array}{l}{b=3}\\{3k+b=0}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BC的表达式为y=-x+3,
∴P(2,1),M(2,3),
∴S△PCM=$\frac{1}{2}$CM•PM=2.
设△QCM的边CM上的高为h,则S△QCM=$\frac{1}{2}$×2×h=2,
∴h=2,
∴Q点的纵坐标为1,
∴-x2+2x+3=1,
解得:x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$(舍去),
∴点Q的坐标为(1+$\sqrt{3}$,1).
(3)过点C作CH⊥MN,垂足为H,如图2所示.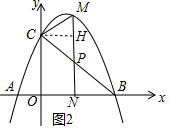
设M(m,-m2+2m+3)(0<m<3),则P(m,-m+3).
∵PM=$\frac{3}{2}$PN,
∴PN=$\frac{2}{5}$MN,
∴-m+3=$\frac{2}{5}$(-m2+2m+3),
解得:m=$\frac{3}{2}$或m=3(舍去),
∴点P 的坐标为($\frac{3}{2}$,$\frac{3}{2}$),M($\frac{3}{2}$,$\frac{15}{4}$),
∴MH=$\frac{15}{4}$-3=$\frac{3}{4}$,CH=$\frac{3}{2}$,
∴tan∠CMN=$\frac{CH}{MH}$=2.
点评 本题考查了待定系数法求一次(二次)函数解析式、二次(一次)函数图象上点的坐标特征、三角形的面积以及解直角三角形,解题的关键是:(1)根据点的坐标利用待定系数法求出函数关系式;(2)根据△QMC和△PMC的面积相等,求出点Q的纵坐标;(3)根据PM=$\frac{3}{2}$PN,求出点P、M的坐标.

 阅读快车系列答案
阅读快车系列答案| A. | 真命题的逆命题是真命题 | |
| B. | 若原命题是假命题,则它的逆命题也是假命题 | |
| C. | 任何一个定理一定有逆定理 | |
| D. | 任何一个命题一定有逆命题 |
| A. | 121×102 | B. | 12.1×103 | C. | 1.21×104 | D. | 0.121×105 |
 如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,若∠A=30°,CD=2,求AC的长.
如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,若∠A=30°,CD=2,求AC的长.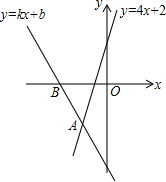 如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.
如图,直线y=kx+b经过点B(-2,0)与直线y=4x+2相交于点A,与y轴交于C(0,-4),则不等式4x+2<kx+b的解集为x<-1.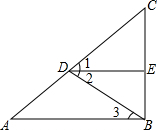 在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,
在下列括号中填写推理理由:如图,∠1=∠2,DE⊥BC,AB⊥BC,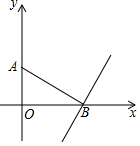 如图,点A(0,3),B(6,0),过点B作AB的垂线l.若直线l上存在点C,满足BC=2$\sqrt{5}$,则点C的坐标为(8,4)或(4,-4).
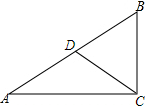
如图,点A(0,3),B(6,0),过点B作AB的垂线l.若直线l上存在点C,满足BC=2$\sqrt{5}$,则点C的坐标为(8,4)或(4,-4). 如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)
如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)