题目内容
17.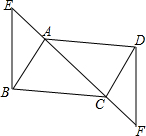 已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)
已知如图,E、F为?ABCD的对角线AC所在直线上的两点,AE=CF,求证:BE=DF.(用两种方法证明)
分析 ①由平行四边形的性质得出AB=CD,∠BAC=∠DCA,由SAS证明△ABE≌△CDF,得出对应边相等即可;
②连接DE、BF,连接BD交AC于O,由平行四边形的性质得出OA=OC,OB=OD,证出OE=OF,得出四边形BFDE是平行四边形,即可得出结论.
解答 证明:方法①:
∵四边形ABCD是平行四边形,
∴AB∥DC,AB=DC.
∴∠BAC=∠DCA.
∴∠BAE=∠DCF,
在△ABE和△CDF中,
$\left\{\begin{array}{l}{AE=CF}&{\;}\\{∠BAE=∠DCF}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(SAS),
∴BE=DF.
方法②:连接DE、BF,连接BD交AC于O,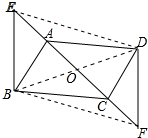 如图所示:
如图所示:
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵AE=CF,
∴OE=OF,
∴四边形BFDE是平行四边形,
∴BE=DF.
点评 本题考查了平行四边形的性质与判定、全等三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形全等和平行四边形是解决问题的关键.

练习册系列答案
相关题目
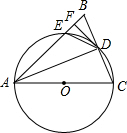 如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,分别交BC、AC于点D、E,连接AD,过点D作DF⊥AB,垂足为点F.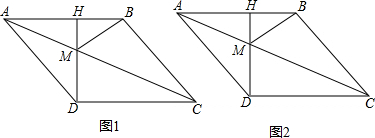
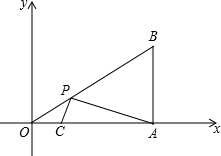 如图,在平面直角坐标系中,Rt△AOB的顶点A在x轴的正半轴上,顶点B的坐标为(3,$\sqrt{3}$),∠OAB=90°,点C的坐标为($\frac{1}{2}$,0),P为斜边OB上一个动点,求△PAC的周长的最小值.
如图,在平面直角坐标系中,Rt△AOB的顶点A在x轴的正半轴上,顶点B的坐标为(3,$\sqrt{3}$),∠OAB=90°,点C的坐标为($\frac{1}{2}$,0),P为斜边OB上一个动点,求△PAC的周长的最小值.